Architektury systemów komputerowych - Lista 4.
Zadanie 1.
Zadanie 2.
Zadanie 3.
Zadanie 4.
Zadanie 5.
Zadanie 6.
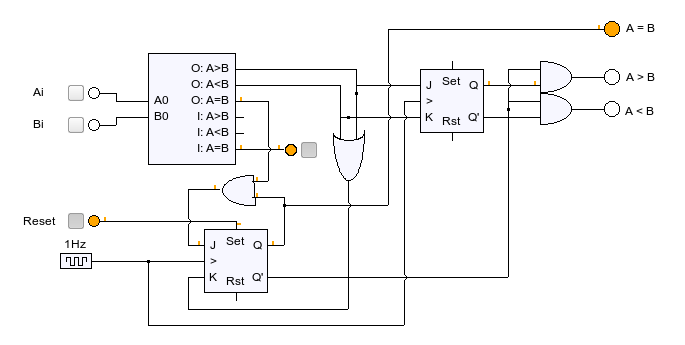
Zadanie 7.
Wykorzystałem tutaj dwa przerzutniki J-K oraz komparator liczb 1-bit (lista 2, zadanie 12). W moim programie do rysowania wspomniany komparator ma wejścia, których nie potrzebujemy (dlatego do „I: A=B” podpinamy 1, do reszty 0)
Zadanie 8.
| X | Y | Q_i | S | Q_{i+1} |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Jest to szeregowy sumator, przyjmujący cyfry od najmniej znaczących. Dzieki przerzutnikowi D zapamietuje carry-bit z poprzedniej operacji.
Zadanie 9.
| X | A_i | B_i | A_{i+1} | B_{i+1} |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
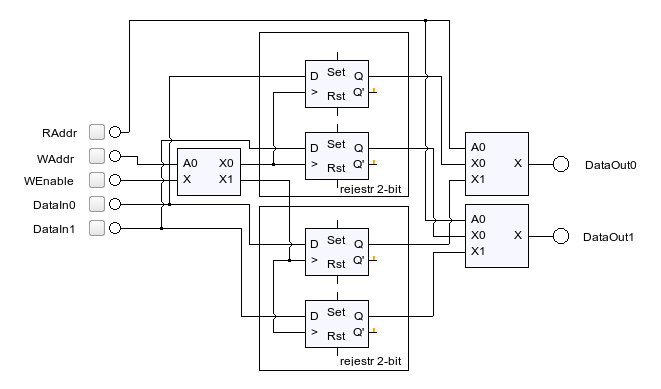
Zadanie 10.
Układ składa się z:
- demultipleksera, do którego jest podłączona linia adresowa zapisu i linia zezwolenia na zapis
- dwóch identycznych rejestrów 2-bit, z wejściami zezwolenia na zapis (podłączone do multipleksera), dwoma bitami zapisywanych danych (podłączone bezpośrednio do linii wejścia) i dwoma bitami wyjścia do odczytu
- dwóch multiplekserów, które zbierają linie wyjścia z rejestrów oraz sterowane bezpośrednio linią adresu odczytu dają wyjścia do odczytu danych
Należy pamiętać, że linia „zezwolenia na zapis” działa tak, jak linia zegarowa - zapis następuje przy zmianie stanu tej linii z 1 na 0 (lub zmianie adresu na demultiplekserze, gdy linia WEnable jest w stanie wysokim).
Rejestry 2-bit są po prostu dwoma przerzutnikami D, z połączoną linią zegarową.
Zadanie 11.
Zauważmy, że:
- wynik może być błędny tylko wtedy, gdy sumowane liczby mają ten sam znak,
- błąd powstaje wtedy, gdy wynik ma inny znak, niż obie sumowane liczby.
W związku z dwoma powyższymi, w ostatnim przerzutniku (najstarszym, odpowiadającym za bit znaku) podpinamy do wejść (x_i, y_i) oraz wyjścia (S_i) odpowiednio kabelki, żeby wyszło nam takie równanie:
err = x_i y_i \bar{S_i} + \bar{x_i} \bar{y_i} S_i
Czyli: błąd powstaje wtedy i tylko wtedy, gdy sumowane liczby mają ten sam znak, różny niż wynik.