Architektury systemów komputerowych - Lista 2.
Zadanie 1.
| a | b | c | d | f(a,b,c,d) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
DNF: Bierzemy wszystkie wartosciowania zmiennych o wartosci funkcji równej 1, i układamy z nich DNF:
a \wedge \neg b \wedge \neg c \wedge \neg d
\vee
\neg a \wedge b \wedge \neg c \wedge \neg d
\vee
\neg a \wedge \neg b \wedge c \wedge \neg d
\vee
\neg a \wedge \neg b \wedge \neg c \wedge d
\vee
a \wedge b \wedge \neg c \wedge \neg d
\vee
a \wedge \neg b \wedge c \wedge \neg d
\vee
a \wedge \neg b \wedge \neg c \wedge d
\vee
\neg a \wedge b \wedge \neg c \wedge d
\vee
\neg a \wedge \neg b \wedge c \wedge d
\vee
a \wedge b \wedge c \wedge \neg d
\vee
a \wedge \neg b \wedge c \wedge d
\vee
a \wedge b \wedge \neg c \wedge d
\vee
a \wedge b \wedge c \wedge d
CNF:bierzemy wartościowania zmiennych, dla których funkcja przyjmuje wartość 0 i robimy z nich DNF i negujemy go
\neg ( (\neg a \wedge \neg b \wedge \neg c \wedge \neg d) \vee (\neg a \wedge b \wedge c \wedge \neg d) \vee (\neg a \wedge b \wedge c \wedge d) )
\equiv
\neg (\neg a \wedge \neg b \wedge \neg c \wedge \neg d) \wedge \neg (\neg a \wedge b \wedge c \wedge \neg d) \wedge \neg (\neg a \wedge b \wedge c \wedge d) )
\equiv
(a \vee b \vee c \vee d) \wedge (a \vee \neg b \vee \neg c \vee d) \wedge (a \vee \neg b \vee \neg c \vee \neg d) )
Zadanie 2.
Nie istnieje taki maxterm, ani minterm, bo z definicji odpowiednio:
- maxtermu, tylko dla jednego wartościowana funkcja przyjmuje 0, a tu przyjmuje dla czterech,
- mintermu, tylko dla jednego wartościowana funkcja przyjmuje 1, a tu przyjmuje dla dwunastu.
Addendum od drx'a: Przyjmujesz definicje z Wikipedii. Kiero smie sie nie zgadzac (w wykladzie) i dopuszcza min/makstermy „czesciowe”.
Wtedy maxterm wymagany w zadaniu to np. x + y.
Wtedy również nie istnieje jeden minterm opisujący 12 jedynek (na poprzedniej liście to omawialiśmy; minterm opisuje 1, 2, 4, 8 albo 16 jedynek).
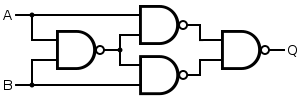
Zadanie 3.
x -.-.-----NAND ~(x&y)
| | NAND-----------------------------NAND ~(x^y) ,--NAND x^y
y -----.-.-NAND NAND--------+ NAND-----
| | | | ,--NAND `--NAND
| | | `-NAND ~y |
| | | NAND-----. |
| | `---NAND `--NAND ~((~x)&(~y)) |
| | NAND--------------'
| `-----NAND ~x .--NAND
| NAND-----'
`-------NAND
Alternatywnie:
Zadanie 4.
x ---XOR x^y
XOR--------XOR x^y^z
y ---XOR XOR-------
,--XOR
z -----------'
Uogólnienie:
a ---XOR a^b^...^z b ---XOR----------- ... XOR z ---XOR
Dowód poprawności:
XOR jest przemienny. Bierzemy pary zer i je odrzucamy. Tak samo z parami jedynek. Zostanie jedno zero lub jedna jedynka. x = {0|1}, y = {0|1}, XOR(x,y,y) = x.
Zadanie 5.
\overline a b \overline c + \overline a b c + a \overline b c = \overline{ \overline{\overline a b \overline c} \cdot \overline{\overline a b c} \cdot \overline{ a \overline b c} } = \uparrow(\uparrow(a\uparrow a,b,c\uparrow c),\uparrow(a\uparrow a,b,c),\uparrow(a,b\uparrow b,c))
Po prawej stronie została użyta notacja prefiksowa.
Zadanie 6.
Z wykładu wiemy, że każda formuła da się zapisać w DNF. Wystarczy więc pokazać, że OR, AND i NOT dają się zapisać jako złożenie NOR (\downarrow).
\overline x = x \downarrow x.
x + y = (x \downarrow y) \downarrow (x \downarrow y)
xy = (x \downarrow x) \downarrow (y \downarrow y)
Zadanie 7.
NAND jest funkcjonalnie zupełny, bo:
x \downarrow y = ( (x \uparrow x) \uparrow (y \uparrow y))\uparrow( (x \uparrow x) \uparrow (y \uparrow y))
A teraz, czemu inne dwuargumentowe funkcje nie są zupełne.
Popatrzmy na tabelki NANDa i NORa:
| x | y | x\uparrow y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| x | y | x\downarrow y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Przez f_{abcd} oznaczymy funkcje ktora przyjmuje odpowiednio a, b, c i d dla argumentow (0,0), (0,1), (1,0), (1,1). Czyli subskrypt jest odzwierciedleniem tabelki logicznej tej funkcji.
- f_{0000} dla samych 0 na wejściu zwraca 0 (nieważne ile razy złożona). Istnieją jednak funkcje, które dla (0,0) zwracają 1. Nie da się ich zbudować przy pomocy tej funkcji.
- f_{0001} dla samych 1 na wejściu zwraca 1 (nieważne ile razy złożona). Istnieją jednak funkcje, które dla (1,1) zwracają 0. Nie da się ich zbudować przy pomocy tej funkcji.
- f_{0010} – patrz f_{0000}.
- f_{0011} – patrz f_{0000} oraz f_{0001}.
- f_{0100} – patrz f_{0000}.
- f_{0101} – patrz f_{0000} oraz f_{0001}.
- f_{0110} – patrz f_{0000}.
- f_{0111} – patrz f_{0000} oraz f_{0001}.
- f_{1000} to NOR.
- f_{1001} – patrz f_{0001}.
- f_{1010} to de facto f(x,y) = \overline y, a NOT nie jest zupełny.
- f_{1011} – patrz f_{0001}.
- f_{1100} to f(x,y) = \overline x, a NOT nie jest zupełny.
- f_{1101} – patrz f_{0001}.
- f_{1110} to NAND.
- f_{1111} – patrz f_{0001}.
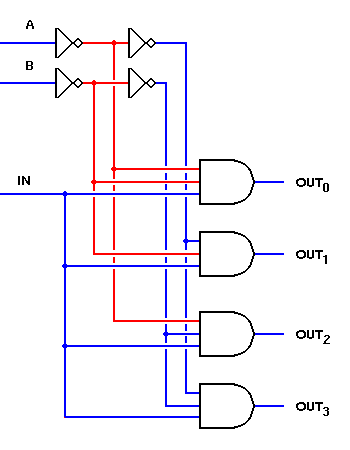
Zadanie 8.
(Obrazek pochodzi ze strony http://www.play-hookey.com/digital/decoder_demux_four.html)
Zadanie 9.
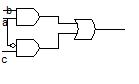
Zadanie 10.
\overline ab + ac
(rozwiazanie z 2008)
(na obrazku c z b mi się jebło, ale to nic nie zmienia)
Bierzemy najpierw a=1 b=1 c=1
Zmieniamy a=0
I przez chwilę górna bramka będzie szybsza, do OR dotrze tylko sygnał 0 z niej i na wyjściu też będzie 0. Zgodnie ze wskazówką NOT przed dolną bramką chwilę zajmuje i zanim sygnał 1 dojdzie do dolnej bramki to przez chwilę na wyjściu będzie błędny wynik.
Zadanie 11.
Można wstawić pustą bramkę logiczną tam gdzie nie ma NOTa.
Zadanie 12.
To co mamy osiągnąć można zapisać w tabelce:
| a | b | a < b | a = b | a > b |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
Czyli:
a < b \equiv \overline a b
a = b \equiv \overline a \cdot \overline b + ab
a > b \equiv a \overline b
Wystarczy to teraz narysować.
Zadanie 13.
Dla a_i, b_i, i \in {0,1,2,3} mamy a_i < b_i, a_i = b_i oraz a_i > b_i z poprzedniego zadania. Przez A i B oznaczymy liczby reprezentowane przez a_i, b_i.
A = B \equiv (a_0=b_0)(a_1=b_1)(a_2=b_2)(a_3=b_3)
A < B \equiv (a_3<b_3) + (a_3=b_3)(a_2<b_2) + (a_3=b_3)(a_2=b_2)(a_1<b_1) + (a_3=b_3)(a_2=b_2)(a_1=b_1)(a_0<b_0)
A > B \equiv (a_3>b_3) + (a_3=b_3)(a_2>b_2) + (a_3=b_3)(a_2=b_2)(a_1>b_1) + (a_3=b_3)(a_2=b_2)(a_1=b_1)(a_0>b_0)