Rachunek prawdopodobieństwa i statystyka - Lista 5.
Zadanie 1
Zadanie 2
Szukamy takiego i, dla którego P(X=i) jest jak największe. Okazuje się, że będzie tak dla i=λ. Dlaczego? Rozkład Poissona ma następującą gęstość:
- Dopóki i jest mniejsze, licznik rośnie cały czas o λ, a mianownik o czynnik mniejszy niż λ - zatem licznik rośnie szybciej.
- Kiedy i osiągnie wartość λ, mianownik zaczyna stopniowo rosnąć o czynniki większe od λ - najpierw λ+1, potem λ+2 itd. Licznik rośnie dalej tak, jak rósł - czyli o λ - już wolniej niż mianownik.
- Zatem maksymalną wartość wyrażenie przyjmie dla i=λ (oraz dla i=λ-1).
- Jeśli λ nie jest liczbą naturalną, to prawdopodobieństwo będzie rosnąć do podłogi z λ.
Zadanie 3
Cała sztuczka polega na tym, by zauważyć, że dla k=0 całe wyrażenie znajdujące się pod sumą wynosi zero, więc możemy sumować od razu od jedynki. Potem tylko przesuniemy granicę sumowania o jeden w dół.
Zadanie 4
Zadanie 5
Tak jak kiedyś różniczkowaliśmy szereg geometryczny, by, przemnażając przez k cały ciąg, otrzymać wzór na wartość oczekiwaną rozkładu geometrycznego, tak teraz będziemy całkować, by podzielić cały szereg przez k.
Całkujemy wzór na szereg geometryczny:
Teraz możemy podstawić wynik całkowania za sumę
Zadanie 6
Aby podstawić
Musimy zrobić dwie rzeczy. Pierwszą jest policzenie wartości bezwzględnej z wyznacznikaMacierzy Jacobiego.
({rcos\theta})'_r & ({rcos\theta})'_\theta\\
({rsin\theta})'_r & ({rsin\theta})'_\theta
\end{vmatrix} = \begin{vmatrix}
cos\theta & -rsin\theta\\
sin\theta & rcos\theta
\end{vmatrix} = rcos^2\theta + rsin^2\theta = r(cos^2\theta+sin^2\theta) = r
Drugą rzeczą jest zmiana granic całkowania. Ponieważ r to promień, może przyjmować wartości od 0 do nieskończoności. Zaś kąt może przyjmować wartości od 0 do 2π. Całka będzie miała postać
Zadanie 7
Z tego, że f jest gęstością wynika, że
Zadanie 8
Zadanie 9
Zadanie 10
Zadanie te można ładnie rozwiązać, rysując kwadrat 1 na 1.
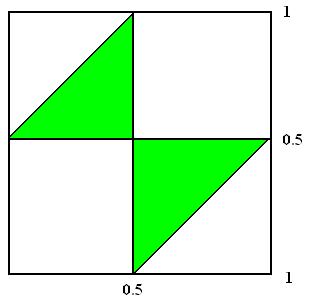
Należy ładnie zapisać warunki, które muszą zachodzić, by wylosowane odcinki mogły utworzyć trójkąt. Będziemy mieli dwa bliźniacze przypadki - gdy x<y i y<x . Jeśli poprawnie wykonamy rysunek, bez trudu obliczymy pole - wyniesie 1/8 + 1/8 = 1/4 .
Zadanie 11
Tutaj też rozpatrujemy dwa przypadki - tyle, że tym razem nie możemy wykręcić się rysunkiem - będziemy musieli policzyć całki:
Pierwsza całka odpowiada bodaj przypadkowi, gdy x<y, a druga przeciwnemu. Nie gwarantuję w 100%, że są poprawne, ale robione są właśnie na taką modłę.