JFiZO - Zadanie 09.024

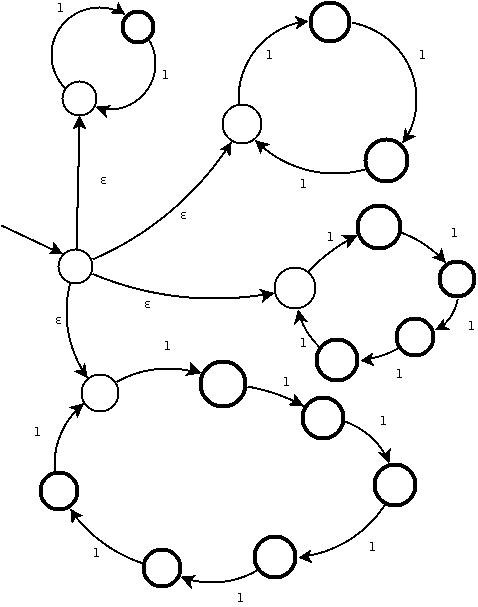
Udowodnij, że istnieje L, który można rozpoznać NDFA o mniej niż 20 stanach, a \overline{L}(dopełnienia) nie da sie rozpoznać NDFA z mniej niż 200 stanami.

L = \{ 1^n : 210 \not{\mid} n \}

\overline L = \{ 1^n : 210 \mid n \}
Załóżmy, że NDFA rozpoznający ten język ma mniej niż 210 stanów.
To znaczy, że podczas czytania słowa 1^{210} jakiś stan wystąpił więcej niż raz.
Można usunąć te przejścia wraz z powtórzonym stanem i akceptacja automatu się nie zmieni.
To znaczy, że automat zakceptuje też słowo 1^a, a < 210, co jest sprzeczne z założeniem, że automat rozpoznaje \overline L.