Spis treści
JFiZO - Zadanie 09.018
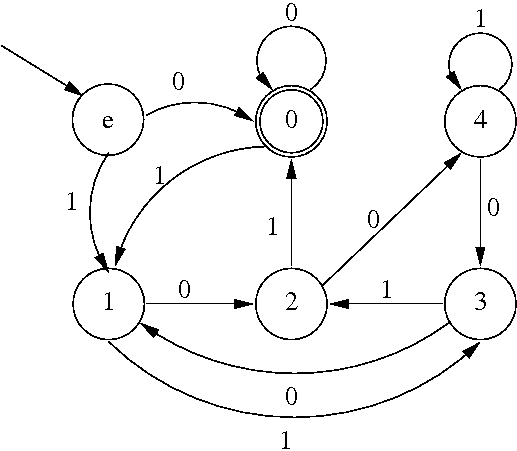
Począwszy od najbardziej znaczącego bitu
Począwszy od najmniej znaczącego bitu
A = (Q, \Sigma, \gamma, F, q_{-1})
- Q = \{q_{ij} : i \in \{1,2,4,3\}, j \in \{0,1,2,3,4\}\} \cup \{q_{-1}\}
- \Sigma = \{0,1\}
- Funkcja przejścia \gamma opisana poniżej
- F = \{q_{i0} : i \in \{1,2,4,3\}\}
- Stan początkowy: q_{-1}
Komentarz:
- startujemy w nieakceptującym q_{-1} (nie chcemy słów pustych).
- 2^i \% 5 = [1,2,4,3,1,2,4,3…] dla kolejnych i, startując od i = 0.
- dla q_{ij} i oznacza, że cyfra którą dopiero wczytaliśmy c jest taka, że c^p \% 5 = i dla potęgi p przy wczytywanej cyfrze. Liczba j oznacza wartość całej liczby którą już wczytaliśmy l modulo 5: l \% 5 = j.
- funkcja f = \{(1,2), (2,4), (4,3), (3,1)\}.
Funkcja przejścia:
- \gamma(q_{i,j}, 0) = q_{f(i),j} - ostatnio wczytany, najbardziej znaczący dotychczas bit, to zero, nie zmienia się wartość całej liczby modulo 5.
- \gamma(q_{i,j}, 1) = q_{f(i),(f(i)+j) \% 5} - ostatnio wczytany, najbardziej znaczący dotychczas bit, to jeden. Nasza nowa liczba to (najstarszy bit do potęgi p, dla odpowiedniego p, plus dotychczasowa liczba) modulo 5.
- \gamma(q_{-1}, i) = q_{1,i}
Począwszy od najmniej znaczącego bitu - podejście 2.
Jakby w rysunku wyżej połączyć stan akceptujący ze stanem e, to też byłoby dobrze, a rozpoznawarke od najmniej znaczącego bitu uzyskalibyśmy odwracając zwroty strzałek przy przejściach.
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji:MIT License