JFiZO - Lista 3
1. Czy istnieje takie wyrażenie regularne \phi, że L_{a\phi} = L_{\phi b}?
Nie.
Załóżmy nie wprost, że istnieje. Rozważmy u\in L_{a\phi}. Wtedy niewątpliwie u \in L_{\phi b}. A więc u zaczyna się od a i kończy na b. Mamy: u = avb dla pewnego v i dodatkowo av \in L_{\phi} (usuwamy końcowe b z wyrazu będącego w L_{\phi b}) oraz vb \in L_{\phi} (usuwamy początkowe a z wyrazu w L_{a\phi}).
Teraz możemy być nieco bardziej bezczelni i napisać, że aav \in L_{a\phi} (dodajemy a na początku wyrazu będącego w L_{\phi}) oraz vbb \in L_{\phi b} (dodajemy b na końcu wyrazu w L_{\phi b}). Och, ale przecież L_{a\phi} = L_{\phi b}, więc aav \in L_{\phi b} oraz vbb \in L_{a\phi}. To by oznaczało, że v = awb dla pewnego w.
Powtarzając powyższe rozumowanie nieskończenie wiele razy moglibyśmy dojść do wniosku, że u=a^\infty b^\infty, ale przecież wyrażenia regularne nie rozpoznają nieskończonych słów. Doprowadzając do sprzeczności kończymy dowód.
2. Czy istnieje takie wyrażenie regularne \phi, że L_{a^*\phi} = L_{\phi b^*}?
Nom.
To wyrażenie to a^*b^*. Jak łatwo zauważyć, L_{a^*\phi} = L_{a^*a^*b^*} = L_{a^*b^*} = L_{a^*b^*b^*} = L_{\phi b^*}.
JFiZO - Zadanie 09.015
a):
- 0^*10^* + 0^* - deterministyczny i niedeterministyczny on-line (np. napisy 00 i 01)
- (0 + 1)^*1(0 + 1) - deterministyczny, ale nie deterministyczny on-line (np. napisy 111 i 1111)
- (0 + 1)(0 + 2)^* + (1 + 2)(0 + 1)^* + (0 + 2)(1 + 2)^* - ani nie deterministyczny (np. napis 0), ani nie deterministyczny on-line (np. napisy 020 i 021)
b):
- 0^*(11^*000^*)^* 11^*01(1+0)^*
- (0+(11^*00))^* 11^*01(1+0)^*
JFiZO - Zadanie 09.016
Język generowany przez (0+1)^*0(0+1) nie posiada deterministycznego on-line wyrażenia regularnego go opisującego.
Pozostaje to udowodnić. 
JFiZO - Zadanie 09.017
- 0^*10^*(10^* + \epsilon)
JFiZO - Zadanie 09.020
Niech L będzie językiem regularnym, a A = (Q, \Sigma, \delta, q_0, F) automatem, który go rozpoznaje. L' = \{ w : \exists n \in \mathbb{N} \, \exists v \in L \, w^n = v \}. Pokażemy, że L' jest językiem regularnym.
Niech Q = \{ 0, 1, \ldots, s\}. Zdefiniujmy automat A' = (Q', \Sigma, \delta', q_0', F'):
- Q' = Q^{s+1},
- q_0' = <0, 1, \ldots, s>,
- \delta'(<i_0, \ldots, i_s>, a) = <\delta(i_0,a), \ldots, \delta(i_s, a)>, więc \hat\delta'(<i_0, \ldots, i_s>, w) = <\hat\delta(i_0, w), \ldots, \hat\delta(i_s, w)>,
- <i_0, \ldots, i_s> \in F' \iff \exists k \, \sigma_k \in F, gdzie \sigma_0 = q_0, \sigma_{k+1} = i_{\sigma_k}.
Przykład stanu akceptującego. Załóżmy, że Q = \{0, 1, 2\}, q_0 = 1 i F = \{2\}. Po wczytaniu pewnego słowa, ze stanu początkowego <0, 1, 2> znaleźliśmy się w przykładowym stanie q = <2, 0, 2>. Sprawdźmy teraz ciąg \sigma. Z definicji wiemy, że \sigma_0 = q_0 = 1. Patrzymy na pozycję 1 i tam jest 0, więc \sigma_1 = 0. Teraz patrzymy na pozycję 0 i tam jest 2 = \sigma_2, które jest stanem akceptującym. Czyli \sigma_k \in F dla k = 2, czyli cała krotka <2, 0, 2> należy do F'. Gdyby q = <0, 0, 2>, to byśmy mieli ciąg:
\sigma_0 = 1 \to \sigma_1 = 0 \to \sigma_2 = 0 \to \sigma_3 = 0 \ldots
Taki stan nie byłby akceptujący.
Twierdzenie. L' = L(A').
Dowód \Rightarrow. Weźmy dowolne w \in L'. Istnieją n i v takie, że w^n = v. Niech q_1, \ldots, q_n będą stanami, w których automat A znajdzie się po wczytaniu słowa w odpowiednio 1 raz, \ldots, n razy. Zauważmy, że \forall i < n \, \hat\delta(q_i, w) = q_{i+1} i q_n \in F. Przyjrzyjmy się teraz, w jakim stanie będzie automat A' po wczytaniu słowa w. Zaczynami w q_0' = <0, 1, \ldots, s>, a po wczytaniu słowa w znaleźliśmy się w jakimś stanie q' = <i_0, \ldots, i_s>. W stanie q' na pozycji q_0 znajduje się stan \hat\delta(q_0, w) = q_1. Zatem \sigma_1 = q_1. Ogólne, \sigma_i = q_i dla i \leq n. Z tego wynika, że \sigma_n = q_n \in F, więc q' \in F'.
Dowód \Leftarrow. Weźmy dowolne w \in L(A'). Automat A' akceptuje słowo w, więc \hat\delta'(q_0', w) = q' \in F'.
Skoro q' \in F', to znaczy, że istnieje takie k, że \sigma_k \in F. Niech q' = <i_0, i_1, \ldots, i_s>.
Lemat. \forall j \leq k \Rightarrow \hat\delta(q_0, w^j) = \sigma_j. Dowód przez indukcję:
- Dla j = 0 mamy \hat\delta(q_0, 0) = q_0 = \sigma_0.
- Niech twierdzenie będzie prawdziwe dla pewnego j < k, czyli \hat\delta(q_0, w^j) = \sigma_j. W q' na pozycji \sigma_j znajduje się \sigma_{j+1} = \hat\delta(\sigma_j, w) = \hat\delta(\hat\delta(q_0, w^j), w) = \hat\delta(q_0, w^{j+1}).
Z lematu wynika, że dla j = k jest \hat\delta(q_0, w^k) = \sigma_k \in F, czyli w^k \in L. Zatem n = k.
JFiZO - Zadanie 09.024
Udowodnij, że istnieje L, który można rozpoznać NDFA o mniej niż 20 stanach, a \overline{L}(dopełnienia) nie da sie rozpoznać NDFA z mniej niż 200 stanami.
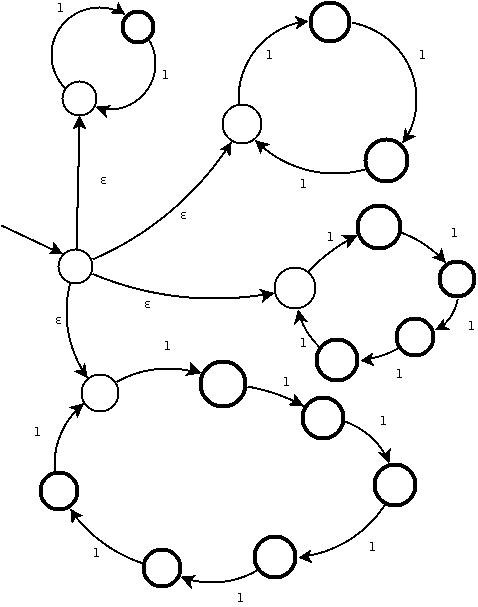
NDFA rozpoznający L
NDFA rozpoznający dopełnienie L
\overline L = \{ 1^n : 210 \mid n \}
Załóżmy, że NDFA rozpoznający ten język ma mniej niż 210 stanów.
To znaczy, że podczas czytania słowa 1^{210} jakiś stan wystąpił więcej niż raz.
Można usunąć te przejścia wraz z powtórzonym stanem i akceptacja automatu się nie zmieni.
To znaczy, że automat zakceptuje też słowo 1^a, a < 210, co jest sprzeczne z założeniem, że automat rozpoznaje \overline L.
JFiZO - Zadanie 09.025
P = \{p: \mathrm{prime}(p)\}.
P_2 = \{2\cdot p: \mathrm{prime}(p) \wedge p > 3\}.
Lemma 1: d(L_k) = k - nie wprost, d(L_k) < k. 0^k - najkrótsze słowo, którego nie akceptujemy. Ale wtedy pewien stan występuje dwukrotnie, więc nie akceptujemy również pewnego słowa 0^l, l < k, sprzeczność.
Lemma 2: n(L_p) = p, p - prime -
Załóżmy, że n( L_p ) < d( L_p ) = p.
Weźmy słowo 0^{p+1}. Należy ono do języka L_p.
To znaczy, że na drodze do stanu akceptującego w automacie powtórzył nam się jakiś stan,
czyli droga stanów wygląda tak q_0 \to \cdots \to q_k \to \cdots \to q_k \to q_e.
Przyjmijmy, że długoś tego cyklu to q. Chcemy tyle razy powtórzyć ten cykl, aby uzyskać false positive.
z - liczba powtórzeń pętli q podczas wczytywania słowa
w \cdot p - wielokrotność p
\exists w,z.(p+1 - q) + z \cdot q = w\cdot p
Istnieje słowo takiej długości, która jest wielokrotnością p
Nie ma różnicy czy z jest większe lub mniejsze o 1, ważne aby było całkowite.
\exists {z' \in \mathbb{N}} \; 1 + z' \cdot q \equiv_p 0
Dodajemy obustronnie p-1
\exists {z' \in \mathbb{N}} \; z \cdot q \equiv_p p - 1
W grupach \mathbb{Z}_p każdy element jest generatorem, czyli w szczególności zawsze osiagniemy p-1 mnożąc q odpowiednio wiele razy.
Uzyskamy wtedy stan akceptujący dla słowa w postaci 0^{wp}, czyli takiego, co nie należy do jeżyka.
Lemma 3: n(L_{2p}) \le 1 + 2 + p, 2p = 2 * p, p - prime, p > 3 - Nie akceptujemy 0^{n} jeśli 2p | n. 2p | n jeśli 2 | n i p | n. Czyli akceptujemy, jesli 2 \not | n lub p \not | n, nasz automat to mucha z wykladu, akceptuje wszedzie oprocz dwoch stanow do ktorych prowadzi epsilon-przejscie ze stanu startowego.
\displaystyle \forall p \in P. \; d(L_p) = n(L_p).
\displaystyle \forall q \in P_2. \; d(L_q) > n(L_q).
JFiZO - Zadanie 09.027
L = \{w: dwa razy więcej zer niż jedynek, i parzysta ilość jedynek\}
- |w|_1 = 2*n
- |w|_0 = 4*n
- |w| = 6*n
L' = S \rightarrow \epsilon | wszystkie permutacje 000011 z poprzeplatanymi S
- L' \subseteq L - trivial
- L \subseteq L' -
- W każdym w \in L istnieje podciąg, który jest permutacją 000011.
- Dowód: niech f(0w) = -1 + f(w), f(1w) = 2 + f(w), f(\epsilon) = 0. Wiemy, że f(w) = 0. Wykazać, że dla każdego w \in L istnieje n t. że f(n) = f(n+6).

- Po usunięciu tego podciągu w dalej \in L.
Inna solucja: Pobawmy się taką gramatyką, która w nieterminalu S ma słowa z naszego języka, a w nieterminalu T słowa podobne - z tą jedynie różnicą, że liczba jedynek jest nieparzysta. No i zauważmy, że S \rightarrow 1T00 | 00T1 | \ldots | 0T0S1 | \ldots | SS, że T \rightarrow coś, no i tu się da rozważyć każdy przypadek i dowód zawierania w obie strony jest za darmo.