JFiZO - Lista 2
JFiZO - Zadanie 09.011
- Regexp1 (błędny): \left(a^* + bb^*(abbb^*)^*aa\right)^*b^*(\epsilon + a + ab)
- Regexp2: (a + b(b + abb)^*aa)^*(\epsilon + b(b+abb)^*(\epsilon + a + ab))
Duży nawias to wszystkie możliwe przejścia ze stanu początkowego ponownie na stan początkowy. Następnie są wszystkie możliwe zakończenia na stanach akceptujących.
JFiZO - Zadanie 09.012
\Sigma = \{a_0, a_1, \ldots, a_n\}. Niech S_k - zbiór wszystkich słów nad alfabetem nie zawierającym słowa a_k:
S_k = \left( \sum_{i \neq k} a_i \right)^*
w_0 = a_0
w_k = (w_{k-1}a_k)^* \cap S_ka_kS_ka_k
Nasze słowo to w_n.
JFiZO - Zadanie 09.013
Rozwiązanie drxa
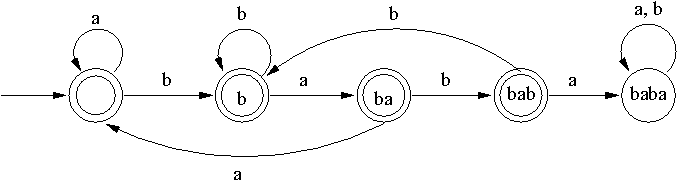
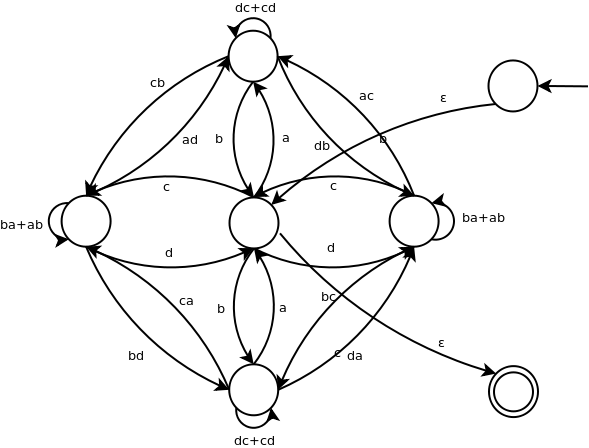
Automat:
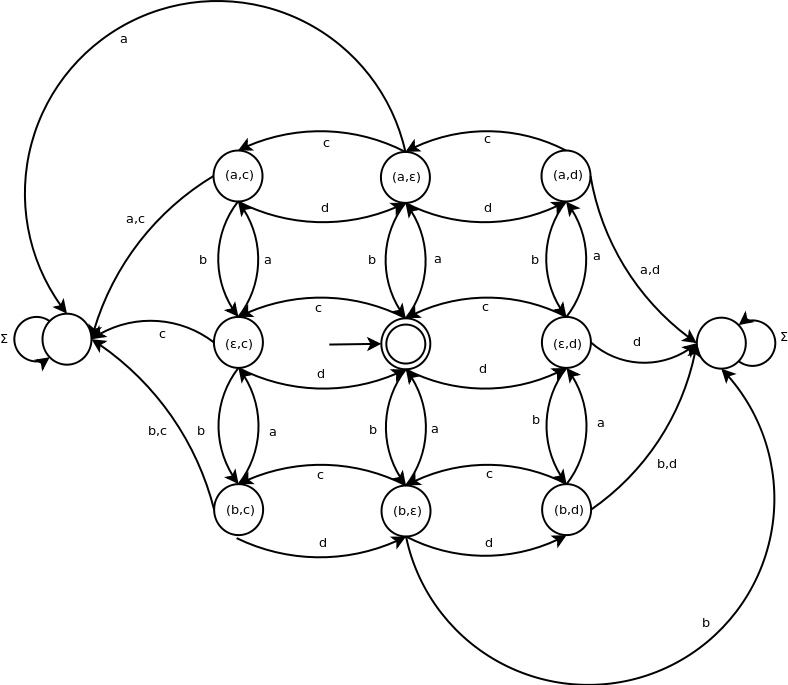
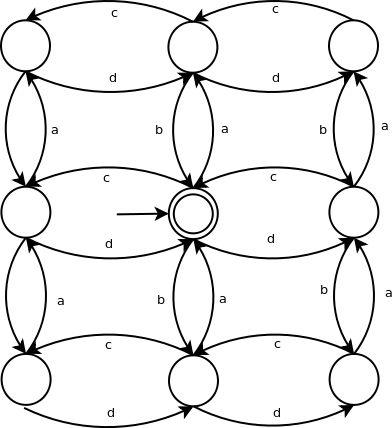
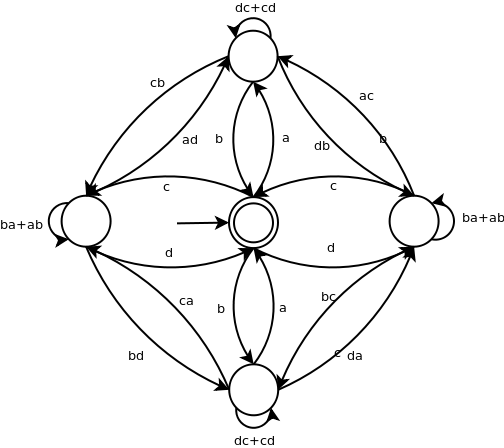
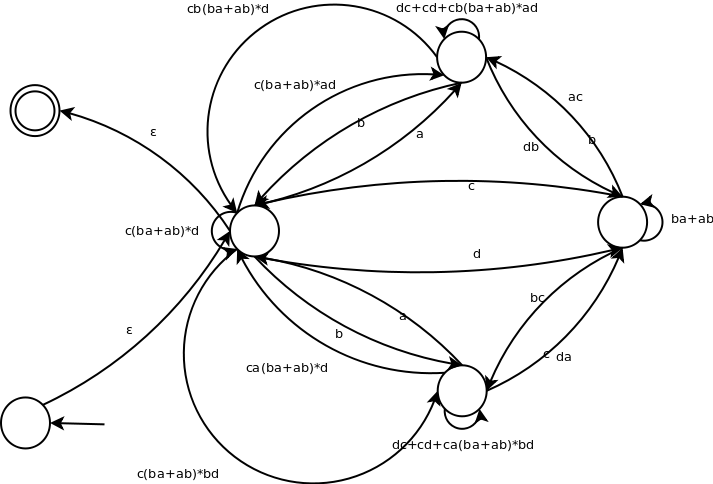
Automat można „zwinąć” w ten sposób:
Na pierwszym grafie usunąłem ścieżki prowadzące do „martwych” stanów. Na drugim „zwinąłem” rogi – usunąłem je (te wierzchołki) jednocześnie wstawiając do grafu krawędzie, które zachowują równoważność z grafem z rogami. Na trzecim grafie zrobiłem osobny stan początkowy i osobny stan końcowy. Na czwartym usunąłem kolejny wierzchołek. Po czym stwierdziłem, że tyle kroków wystarczy by zobaczyć sens algorytmu, a efekt końcowy będzie równie nieczytelny co skrypt perlowy dude'a, więc pozostawię usunięcie reszty zbędnych wierzchołków czytelnikowi (ew. komuś przy tablicy).
Niekompletne rozwiązanie Tomsika
\left(a(dc+cd)^*b+b(dc+cd)^*a+c(ab+ba)^*d+d(ab+ba)^*c + adbc + bdac + acbd + bcad + cadb + dacb + cbda + dbca\right)^*
 Nie przechodzi adbacb
Nie przechodzi adbacb
Gówniane rozwiązanie dude'a
Wygenerowane programem w perlu, lol http://dude.bshellz.net/zad13.pl
- regexp: (cd + ba + dc + ab + (bd + db)(cd + ab)*(ca + ac) + (cb + bc + (bd + db)(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(ad + da + dd(cd + ab)*(ca + ac)) + (da + ad + (bd + db)(cd + ab)*aa + (cb + bc + (bd + db)(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))(ba + cd + bb(cd + ab)*aa + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))*(bc + cb + bb(cd + ab)*(ca + ac) + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(ad + da + dd(cd + ab)*(ca + ac))) + (ca + ac + (cb + bc + (bd + db)(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*aa + (da + ad + (bd + db)(cd + ab)*aa + (cb + bc + (bd + db)(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))(ba + cd + bb(cd + ab)*aa + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))*(cc + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*aa))(ba + dc + bb(ab + dc + dd(cd + ab)*cc)*aa + (dd + bb(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))(ba + cd + bb(cd + ab)*aa + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))*(cc + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*aa))*(bd + db + bb(ab + dc + dd(cd + ab)*cc)*(ad + da + dd(cd + ab)*(ca + ac)) + (dd + bb(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))(ba + cd + bb(cd + ab)*aa + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(dd(cd + ab)*aa))*(bc + cb + bb(cd + ab)*(ca + ac) + (bb(cd + ab)*cc)(ab + dc + dd(cd + ab)*cc)*(ad + da + dd(cd + ab)*(ca + ac)))))*
- kod:
#!/usr/bin/perl -w
use strict;
my $start;
my $finish;
my %trans;
while (<>) {
chomp;
next if !$_;
if (/^S:\s*(\(.*\))/) {
$start = $1;
} elsif (/^F:\s*(\(.*\))/) {
$finish = $1;
} elsif (/(\(.*?\))\s*-(.*?)>\s*(\(.*?\))/) {
if ($trans{$1}->{$3}) {
$trans{$1}->{$3} .= " + $2";
} else {
$trans{$1}->{$3} = "$2";
}
}
}
while (keys %trans > 1) {
for my $toremove (keys %{$trans{$start}}) {
next if $toremove eq $start;
my $loop = "";
if ($trans{$toremove}->{$toremove}) {
$loop = "($trans{$toremove}->{$toremove})*";
}
for my $neigh (keys %trans) {
next if $neigh eq $toremove;
next unless ($trans{$neigh}->{$toremove});
my $via = $trans{$neigh}->{$toremove};
$via = "($via)" if ($via =~ /(\+\s)/);
for my $dist (keys %{$trans{$toremove}}) {
next if $dist eq $toremove;
my $via2 = $trans{$toremove}->{$dist};
$via2 = "($via2)" if ($via2 =~ /(\+\s)/);
my $path = "$via$loop$via2";
if ($trans{$neigh}->{$dist}) {
$trans{$neigh}->{$dist} .= " + $path";
} else {
$trans{$neigh}->{$dist} = "$path";
}
}
delete $trans{$neigh}->{$toremove};
}
delete $trans{$toremove};
}
}
my $loop = "";
if ($trans{$start}->{$start}) {
$loop = "($trans{$start}->{$start})*";
}
my $path = "";
if ($trans{$start}->{$finish}) {
$path = $trans{$start}->{$finish};
}
$path = "$loop$path";
$path =~ s/e([a-df-z]+)/$1/g;
$path =~ s/([a-df-z]+)e/$1/g;
print "$path\n";
- automat:
S: ( 0, 0) F: (A) ( 0, 0) -a> ( 1, 0) ( 0, 0) -b> (-1, 0) ( 0, 0) -c> ( 0, 1) ( 0, 0) -d> ( 0,-1) ( 0, 0) -e> (A) ( 1, 0) -a> (F) ( 1, 0) -b> ( 0, 0) ( 1, 0) -c> ( 1, 1) ( 1, 0) -d> ( 1,-1) (-1, 0) -a> ( 0, 0) (-1, 0) -b> (F) (-1, 0) -c> (-1, 1) (-1, 0) -d> (-1,-1) ( 0, 1) -a> ( 1, 1) ( 0, 1) -b> (-1, 1) ( 0, 1) -c> (F) ( 0, 1) -d> ( 0, 0) ( 0,-1) -a> ( 1,-1) ( 0,-1) -b> (-1,-1) ( 0,-1) -c> ( 0, 0) ( 0,-1) -d> (F) ( 1, 1) -a> (F) ( 1, 1) -b> ( 0, 1) ( 1, 1) -c> (F) ( 1, 1) -d> ( 1, 0) ( 1,-1) -a> (F) ( 1,-1) -b> ( 0,-1) ( 1,-1) -c> ( 1, 0) ( 1,-1) -d> (F) (-1, 1) -a> ( 0, 1) (-1, 1) -b> (F) (-1, 1) -c> (F) (-1, 1) -d> (-1, 0) (-1,-1) -a> ( 0,-1) (-1,-1) -b> (F) (-1,-1) -c> (-1, 0) (-1,-1) -d> (F)
Łatwo zauważyć, że możemy bez problemu rozpoznać język L_p', który działa dokładnie tak samo, z taką różnicą, że wczytujemy słowa od lewej (od najbardziej znaczącego bitu).
Widzimy, że L_p' = \{ w^R | w \in L_p \} i skorzystamy z tego, że NDFA się łatwo odwracają. Pokażę teraz krótko konstrukcję automatu rozpoznającego odwrócony język.
Niech A = \langle \Sigma, Q, q_0, F, \delta \rangle, to A^R = \langle \Sigma, Q \cup \{q_z\}, q_z, \{q_0\}, \delta' \}. Idea konstrukcji jest taka:
- q_z jest dodatkowym stanem, od którego będziemy startować
- od q_z idą epsilon-przejścia do każdego stanu akceptującego automatu A
- potem łazimy po stanach A przy czym po odwróconych krawędziach
- stanem akceptującym jest q_0
Formalniej,
- \delta'(q_z, \epsilon, q) \Leftarrow q \in F
- \delta'(q, a, q') \Leftarrow \delta(q', a, q)
Innymi słowy, jesteśmy w stanie rozpoznać odwrócony język używając jednego stanu więcej.
No dobrze, uzbrojeni w tą wiedzę, możemy krótko opisać automat z zadania. Nietrudno skonstruować NDFA (a nawet DFA) rozpoznający L_p'. Niech Q = \{q_0\} \cup \{0, \ldots, p-1\}, krawędzie zaś są postaci: \delta(q_0, a) = a \wedge \delta(r, a) = (2r + a) mod\ p, gdzie oczywiście a \in \{0,1\}. Automat na p+1 stanów, także ten rozpoznający odwrócony - p+2. Koniec.