Analiza numeryczna (M) - Lista 4.
Zadanie 1.
Metoda iteracyjna: x_{k+1}= F ( x_k )
Jest zbieżna do pierwiastka \alpha w równaniu f(x) = 0
F(\alpha)=\alpha oraz 0 = F'(\alpha)=…=F^{(p-1)}(\alpha) \not = F^{(p)}(\alpha)
niech: e_{n+1} = x_{n+1} - \alpha = F ( x_n ) - \alpha
zapisując funkcję F wzorem Taylora (Reszta w postaci Lagrange'a):
F(x) =\displaystyle F(\alpha) + \left( \sum _ {k=1} ^{p-1} \frac {(x - \alpha)^k}{k!}F^{(k)}(\alpha) \right) + \frac {(x - \alpha ) ^ p}{p!} F^{(p)}( \xi ) = \frac {(x - \alpha ) ^ p}{p!} F^{(p)}( \xi ) + \alpha
Więc:
e_{n+1} = \frac {(x_n - \alpha ) ^ p}{p!} F^{(p)}( \xi )
e_{n+1} = \displaystyle \frac {e_n^ p}{p!} F^{(p)}( \xi )
a stąd już widzimy, że:
\displaystyle\frac{e_{n+1}}{e_n^p} = \frac{1}{p!}F^{(p)}( \xi )
Czyli owa metoda iteracyjna ma rząd = p. :3
Zadanie 2.
W uproszczonej metodzie Newtona definiujemy: x_{n+1} = x_n - \frac{f(x_n)}{f'(x_0)} , e_n = x_n - \alpha stąd:
e_{n+1} = e_{n} - \frac{f(x_n)}{f'(x_0))} = e_{n} - \frac{f(e_n + \alpha)}{f'(x_0)}
Ponieważ \alpha jest pojedynczym zerem, to f(\alpha) = 0 oraz f'(\alpha) \not = 0
Rozwijamy licznik i mianownik we wzoru taylora: e_{n+1} = e_{n} - \frac{f(\alpha) + f'(\alpha +\theta e_n)e_n }{f'(x_0)} = e_{n} - \frac{f'(\alpha +\theta e_n)e_n }{f'(x_0)}
więc….
\frac{e_{n+1}}{e_n} = 1 - \frac{f'(\alpha +\theta e_n)}{f'(x_0)} \rightarrow 1 - \frac{f'(\alpha)}{f'(x_0)} Stąd widzimy, że wersja uproszczona metody newtona dla zera pojedynczego jest zbieżna liniowo :3
Zadanie 3.
W metodzie Newtona definiujemy: x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} , e_n = x_n - \alpha stąd:
e_{n+1} = e_{n} - \frac{f(x_n)}{f'(x_n)} = e_{n} - \frac{f(e_n + \alpha)}{f'(e_n + \alpha)}
Ponieważ \alpha jest podwójnym zerem, to f(\alpha) = f'(\alpha) = 0 oraz f”(\alpha) \not = 0
Rozwijamy licznik i mianownik we wzór taylora:
e_{n+1} = e_{n} - \frac{f(\alpha) + f'(\alpha)e_n + f(\alpha + \theta e_n)e_n^2 }{f'(\alpha) + f(\alpha + \theta e_n)e_n }
więc….
\frac{e_{n+1}}{e_n} = 1 - \frac{\frac{1}{2}f(\alpha + \theta e_n)e_n}{f(\alpha + \theta e_n)e_n} = 1 - \frac{\frac{1}{2}f(\alpha + \theta e_n)}{f(\alpha + \theta e_n)}
A to przy n \to \infty , e_n \to 0 daje:
\frac{e_{n+1}}{e_n} \rightarrow 1 - \frac{1}{2} = \frac{1}{2}
Czyli metoda Newtona dla zera podwójnego jest zbieżna liniowo :3
Zadanie 4.
4.) Jedynym miejscem zerowym funkcji \frac{1}{x} - R = 0 jest x = \frac{1}{R} czyli nasza szukana odwrotność. Więc:
\displaystyle h_n = \frac{\frac{1}{x} - R}{(\frac{1}{x} - R)'} = \frac{\frac{1}{x} - R}{\frac{1}{-x^2}} = Rx^2 - x
Metoda Newtona definiuje wzór rekurencyjny:
\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - h_n
czyli:
\displaystyle x_{n+1} = x_n - (Rx_n^2 - x_n) = x_n(2 - Rx_n)
[b]b) zbieżność[/b], styczna do wykresu w punkcie będzie miała wzór:
wzór ogólny: y-y_0 = f'(x_0)(x-x_0) , mega wzór:
\displaystyle y - f(x_0) = \frac{1}{-x_0^2}(x-x_0)
\displaystyle y = \frac{x}{-x_0^2} + \frac{1}{x_0} + \frac{1}{x_0} - R
\displaystyle y = \frac{x}{-x_0^2} + \frac{2}{x_0} - R
Rozpatrzmy R > 0, pierwiastek \alpha jest wtedy po prawej stronie osi Y. Obserwując jak zachowują się styczne do wykresu w pobliżu \alpha dochodzimy do wniosku, że x_0 > 0, oraz styczna w punkcie x_0 nie może przeciąć ujemnej części osi X.
Zatem: x_0 \in (0,\beta) ,
gdzie \beta = \max (p_1,p_2)
\displaystyle 0 = \frac{x}{-x_0^2} + \frac{2}{x_0} - R
\displaystyle Rx_0^2 = 2x_0-x
\displaystyle x = 2x_0 -Rx_0^2
\displaystyle 0 = -Rx_0^2 + 2x_0
rozwiązujemy równanie kwadratowe:
\sqrt{\Delta} = 2
\displaystyle p_1 = \frac{-2 +2}{-2R}=0 oraz \displaystyle p_2 = \frac{-2-2}{-2R} = \frac{2}{R}
Zatem \displaystyle x_0 \in (0,\frac{2}{R}) dla R>0 oraz
\displaystyle x_0 \in (-\frac{2}{R},0) dla R<0 gdyz przypadki są symetryczne…
Zadanie 5.
5.) Chcemy efektywnie odnajdywać wartość \sqrt{a} .
\displaystyle \sqrt{a} = x
\displaystyle a = x^2
\displaystyle x^2 - a = 0
Niech f(x)=x^2-a .
Wykorzystamy metode Newtona do odnalezienia miejsca zerowego tej funkcji. \displaystyle f'(x) = (x^2 - a)' = 2\cdot x
\displaystyle x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{x_n^2 - a}{2\cdot x_n} = \frac{2\cdot x_n^2 - x_n^2 + a}{2\cdot x_n} =\frac{x_n^2 + a}{2\cdot x_n} = \frac{1}{2}\cdot (x_n + \frac{a}{x_n})
[b]b) zbieżność:[/b] Jeśli naszkicujemy wykres funkcji f(x)=x^2-a widzimy, że jest wykresem paraboli przesuniętej w górę/dół o a, a pierwiastkiem który nas interesuje jest ten po prawej.. :p zatem żeby metoda newtona nie zeszła nam na zły pierwiastek, spełnione musi być: x_0 > 0. Bo: w punkcie x_0=0 styczna jest równoległa do osi współrzędnych więc jest oj źle, a ponieważ funkcja jest wklęsła to styczne będą „na zewnątrz” więc nie przetną „złej połówki” paraboli…
Pomijając ścianę tekstu, funkcja jest zbieżna dla wszystkich x_0 takich, że x_0>0.
Zadanie 6.
6.) r-krotne zero \alpha funkcji f(x) jest pojedynczym zerem funkcji g(x)=\sqrt[r]{f(x)} zatem \displaystyle f(x) = (\alpha - x)^r R \displaystyle g(x) = \sqrt[r]{(\alpha - x)^r R} = (\alpha - x)\sqrt[r]{R}
\alpha jest pojedynczym zerem funkcji g(x), zatem g(\alpha)=0 oraz g'(\alpha) \not = 0 ..
wiemy, że: \displaystyle g'(x) = (\sqrt[r]{f(x)})' = \frac{1}{r} \cdot (f(x))^{\frac{1}{r}-1} \cdot f'(x) = \frac{1}{r} \cdot (f(x))^{\frac{1-r}{r}} \cdot f'(x)
\displaystyle x_{n+1} = x_n - \frac{\sqrt[r]{f(x)}}{(\sqrt[r]{f(x)})'} = x_n - \frac{\sqrt[r]{f(x)}}{\frac{1}{r} \cdot (f(x))^{\frac{1-r}{r}} \cdot f'(x) } = x_n - \frac{r \cdot (f(x))^{\frac{1}{r}} \cdot (f(x))^{\frac{r-1}{r}} }{f'(x)} = x_n - r\cdot \frac{f(x)}{f'(x)}
ponad to: \displaystyle f'(x) = R (\alpha-x)^r \left(\frac{-r}{\alpha-x} \right) + (\alpha -x)^ r R'(x) więc: \displaystyle x_{n+1} = x_n - r\cdot \frac{R(\alpha-x_n)^r}{R (\alpha-x)^r \left(\frac{-r}{\alpha-x} \right) + (\alpha -x)^ r R'(x)} = x_n - r\cdot \frac{R}{R\left(\frac{-r}{\alpha-x} \right) + R'(x)}
Zadanie 7.
7.) Mamy jakąs funkcje f o której wiemy że: f'(x)>0
f' '(x)>0
f( a ) = 0 dla x \in R
Mamy wykazać że a to jedyny pierwiastek:
Mamy wykazać że metoda Newtona daje ciąg do niego zbieżny: [i][rozwiązanie zaczerpnięte z Kincaid'a tw3.2.3 strona pdf 95][/i]
Z Analizy Matematycznej wiemy że skoro f''(x)>0 to f jest wypukła (???) . Ponieważ f'(x) > 0 to f jest rosnąca. Z wzoru na e_{n+1}
e_{n+1}=\frac{1}{2} \cdot e_n^2 \cdot \frac{f' '(i)}{f'(x_n)}
wnioskujemy że e_{n+1} > 0, a wzwiazku z tym ponieważ e_n = x_n - a to x_n > a dla n \ge 1
Z powyższego wniosku i z tego że f jest rosnąca wynika że f(x_n) > f(a) = 0
Wiemy że e_{n+1}=x_{n+1}-a = x_n - a - \frac{f(x_n)}{f'(x_n)} = e_n - \frac{f(x_n)}{f'(x_n)} więc e_{n+1} < e_n
Tak więc ciągi e_n i x_n są malejące i ograniczone z dołu więc metoda Newtona jest zbieżna.
Zadanie 8.
f(x) = cos^22x - x^2
f'(x) = 2cos(2x) \cdot (cos(2x))' - 2x = 2cos(2x) \cdot (-sin(2x)\cdot2) - 2x = -4cos(2x)sin(2x) -2x
Wygenerowane porównanie tych metod które ja znam (wykresy niech ktoś kto umie gnuplota używać dorobi):
Metoda Newtona (stycznych), x0 = 0.75
| n | x_n | |x_n-a| |
|---|---|---|
| 1 | 0.437193507464 | 0.077739757236 |
| 2 | 0.514702467893 | 0.000230796807 |
| 3 | 0.514933247961 | 0.000000016739 |
Metoda siecznych, x0 = 0.75 x1 = 0.00
| n | x_n | |x_n-a| |
|---|---|---|
| 1 | 0.481542090916 | 0.033391173784 |
| 2 | 0.531590029425 | 0.016656764725 |
| 3 | 0.515091416040 | 0.000158151340 |
| 4 | 0.514932357449 | 0.000000907251 |
| 5 | 0.514933264706 | 0.000000000006 |
Metoda regula falsi, a = 0.00 b = 0.75
| n | x_n | |x_n-a| |
|---|---|---|
| 1 | 0.520328114213 | 0.005394849513 |
| 2 | 0.512610677322 | 0.002322587378 |
| 3 | 0.515345545463 | 0.000412280763 |
| 4 | 0.514752347689 | 0.000180917011 |
| 5 | 0.514965582436 | 0.000032317736 |
| 6 | 0.514919062353 | 0.000014202347 |
| 7 | 0.514935802909 | 0.000002538209 |
| 8 | 0.514932149080 | 0.000001115620 |
| 9 | 0.514933464046 | 0.000000199346 |
| 10 | 0.514933177029 | 0.000000087671 |
Metoda bisekcji, a = 0.00 b = 0.75
| n | x_n | |x_n-a| |
|---|---|---|
| 1 | 0.375000000000 | 0.139933264700 |
| 2 | 0.562500000000 | 0.047566735300 |
| 3 | 0.468750000000 | 0.046183264700 |
| 4 | 0.515625000000 | 0.000691735300 |
| 5 | 0.492187500000 | 0.022745764700 |
| 6 | 0.503906250000 | 0.011027014700 |
| 7 | 0.509765625000 | 0.005167639700 |
| 8 | 0.512695312500 | 0.002237952200 |
| 9 | 0.514160156250 | 0.000773108450 |
| 10 | 0.514892578125 | 0.000040686575 |
| 11 | 0.515258789063 | 0.000325524362 |
| 12 | 0.515075683594 | 0.000142418894 |
| 13 | 0.514984130859 | 0.000050866159 |
| 14 | 0.514938354492 | 0.000005089792 |
| 15 | 0.514915466309 | 0.000017798391 |
| 16 | 0.514926910400 | 0.000006354300 |
| 17 | 0.514932632446 | 0.000000632254 |
| 18 | 0.514935493469 | 0.000002228769 |
| 19 | 0.514934062958 | 0.000000798258 |
| 20 | 0.514933347702 | 0.000000083002 |
| 21 | 0.514932990074 | 0.000000274626 |
| 22 | 0.514933168888 | 0.000000095812 |
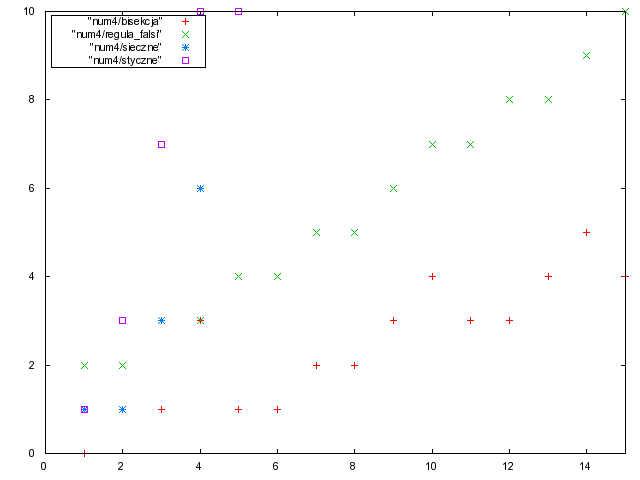
zależność cyfr znaczących poprawnych od liczby iteracji
gnuplot to dzieło szatana
# -*- coding: utf-8 -*- # """ @copyright: 2009 by Piotr Rzepecki <me@vanzi.info> @license: GNU GPL, see COPYING for details. """ from math import * eps = pow(10,-7) alfa = 0.5149332647 def f(x): return pow(cos(2*x),2) - pow(x,2) def f1(x): return -4*sin(2*x)*cos(2*x) - 2*x def metoda_newtona(x0): n = 0 xn = x0 print ("Metoda Newtona (stycznych), x0 = %.2f\nn\tx_n\t\t|x_n-a|" % x0) while (abs(xn - alfa) >= eps): xn = xn - (f(xn))/(f1(xn)) n += 1 print ("%d\t%.12f\t%.12f" % (n,xn,abs(xn-alfa))) return xn def metoda_siecznych(x0,x1): print ("Metoda siecznych, x0 = %.2f x1 = %.2f\nn\tx_n\t\t|x_n-a|" % (x0,x1)) xn = x0 xn1 = x1 n = 0 while (abs(xn1-alfa) >= eps): t = xn1 xn1 = xn1 - f(xn1)*(xn1-xn)/(f(xn1) - f(xn)) xn = t n += 1 print ("%d\t%.12f\t%.12f" % (n,xn1,abs(xn1-alfa))) return xn1 def metoda_regula_falsi(a,b): print ("Metoda regula falsi, a = %.2f b = %.2f\nn\tx_n\t\t|x_n-a|" % (a,b)) xn = (a*f(b) - b*f(a))/(f(b) - f(a)) n = 0 while (abs(xn-alfa) >= eps): if f(a)*f(xn) <= 0: xn = (xn*f(a) - a*f(xn))/(f(a) - f(xn)) else: xn = (xn*f(b) - b*f(xn))/(f(b) - f(xn)) n += 1 print ("%d\t%.12f\t%.12f" % (n,xn,abs(xn-alfa))) return xn def metoda_bisekcji(a,b): print ("Metoda bisekcji, a = %.2f b = %.2f\nn\tm_n\t\t|m_n-a|" % (a,b)) n = 0 while (abs((a-b)/2) >= eps): mn = (a+b)/2 if f(a)*f(mn) < 0: b = mn else: a = mn n+=1 print ("%d\t%.12f\t%.12f" % (n,mn,abs(mn-alfa))) return (a+b)/2 metoda_newtona(0.75) metoda_siecznych(0.75,0.) metoda_regula_falsi(0.,0.75) metoda_bisekcji(0.,0.75)
Dyskusja
Ad3. Skąd (w linijce zaczynającej się słowem „Więc…”) pojawiła się nagle 1/2 oraz dlaczego jest to f(costam) zamiast f”(costam)?