Spis treści
Analiza matematyczna - Lista 1.
Zadanie 1
- u = x + \sqrt{y}
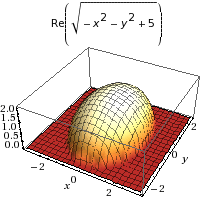
y \geq 0 - u = \sqrt{1 - x^2 - y^2}
1-x^2-y^2 \geq 0
1 \geq x^2+y^2 - u = \sqrt{1-x^2} + \sqrt{y^2-1}
1-x^2 \geq 0 \wedge y^2-1 \geq 0
|x| \leq 1 \wedge |y| \geq 1 - u = \frac 1 {\sqrt{x^2+y^2-1}}
x^2+y^2 > 1 - boring
- boring
- u = \arcsin \frac y x
\frac y x \geq -1 \wedge \frac y x \leq 1 \wedge x \neq 0
y \geq -x \wedge y \leq x \wedge x \neq 0
Zadanie 2
Zadanie 3
Zadanie 4
- \lim_{(x,y)→0} \frac x {x+y} |_{x=y} = \frac 1 2
\lim_{(x,y)→0} \frac x {x+y} |_{y=0} = 1 - \lim_{(x,y)→0} \frac {2xy} {x^2+y^2} |_{x=y} = 1
\lim_{(x,y)→0} \frac {2xy} {x^2+y^2} |_{x=3y} = \frac 6 {10} - \lim_{(x,y)→(0,1)} \frac {x^6} {y^2-1} |_{y=x+1} = 1 cdn
Zadanie 5
Zadanie 6
Zadanie 7
Zadanie 8
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji:MIT License