Analiza numeryczna (M) - Lista 3.
* Lista 3.
Zadanie 1.
Można to zrobić bez użycia indukcji, ale dla nie wszystkich to może być oczywiste, więc bedzie indukcja.
n = 1. \displaystyle \prod_{i=1}^1{(1+\varepsilon_i)} = 1+\varepsilon_1 = 1+\sigma_1
n > 1. \displaystyle \prod_{i=1}^n{(1+\varepsilon_i)} = (1 + \sigma_{n-1})(1 + \varepsilon_n) = 1 + \sigma_{n-1} + \varepsilon_n + \sigma_{n-1}\cdot\varepsilon_n = 1 + \sigma_{n} + (\varepsilon_1\cdot\varepsilon_n + \varepsilon_2\cdot\varepsilon_n + \cdots + \varepsilon_{n-1}\cdot\varepsilon_n + O(2^{-2t})\cdot\varepsilon_n) \buildrel{(*)}\over{=} 1 + \sigma_n
(*) Każdy z czynników \varepsilon_i\cdot\varepsilon_n (dla i < n) jest mniejszy od 2^{-t}\cdot2^{-t} = 2^{-2t}, więc można je wrzucić „pod” O(2^{-2t}) z \sigma_n.
Zadanie 2.
\displaystyle |\sigma_n| \leq |\varepsilon_1| + |\varepsilon_2| + \cdots + |\varepsilon_n| + O(2^{-2t}) \buildrel{(2)}\over\leq n\cdot2^{-t} + O(2^{-2t}) \buildrel{(1)}\over\leq \frac{n2^{-t}}{1 - \frac 1 2 n 2^{-t}} = \omega_n
(1) Ponieważ n < 2\cdot2^t, zawsze zachodzi 1 - \frac 1 2 n 2^{-t} < 1. Mianownik zwiększa więc cały ułamek, w dodatku bardziej niż dodanie O(2^{-2t}).
(2) Przyda sie w zadaniu 3.
edit: dotlumaczenie (1):
n\cdot2^{-t} + O(2^{-2t}) \leq \frac{n2^{-t}}{1 - \frac 1 2 n 2^{-t}}
\displaystyle O(2^{-2t}) \leq \frac{n2^{-t} - n2^{-t}(1 - \frac 1 2 n 2^{-t})}{1 - \frac 1 2 n 2^{-t}} = \frac{ \frac 1 2 n^2 2^{-2t} }{1 - \frac 1 2 n 2^{-t}} = \frac{ O(1) } { 1 - \frac 1 2 n 2^{-t} } (a to juz jest dosyc oczywiste)
Zadanie 3.
Ma być \omega_n \leq n ( 1.06 \cdot 2^{-t} ), czyli mianownik \omega_n powinien zwiększać całośc ułamka o mniej niż 1.06, czyli powinien być większy od \frac 1 {1.06} \approx 0.943.
1- \frac 1 2 n 2^{-t} > 0.943
Czyli musi zachodzić \frac 1 2 n 2^{-t} < 0.057 . Sprawdźmy:
\frac 1 2 n 2^{-t} < \frac 1 2 \cdot (0.1) \cdot 2^t \cdot 2^{-t} = 0.05 < 0.057. OK.
Teraz pozostaje wywnioskować drugą nierówność:
\sigma_n \leq \omega_n \leq n (1.06 \cdot 2^{-t}) = n \cdot 2^{-t + \log(1.06)} = n \cdot 2^{-t + 0.08406} \buildrel{<}\over{\sim} n \cdot 2^{-t}
Troche komentarza: ostatnia nierówność jest dlatego, że różnica w wykładniku rzędu -0.08 niewiele zmienia przebieg funkcji. Patrz notatki z wykładu.
Ten wniosek można było również wyciągnąc patrząc po prostu na wzór \sigma_n. Jak widać, zaburzeniem nierówności jest O(2^{-2t}).
Zadanie 4.
\overline s_0 = 0
\overline s_k = \overline s_{k-1}(1+\varepsilon_{2k+1}) + x_ky_k(1+\varepsilon_{2k})(1+\varepsilon_{2k+1})
\overline s_n = \displaystyle \sum_{i=0}^{n}{x_iy_i( 1 + \varepsilon_{2i} )(\prod_{j=0}^i{(1+\varepsilon_{2j+1})})} \approx \sum_{i=0}^{n}{x_iy_i( 1 + \varepsilon_{2i} )(1 + \varepsilon_1 + \varepsilon_3 + \cdots + \varepsilon_{2i+1})} \approx \sum_{i=0}^{n}{x_iy_i(1 + \varepsilon_1 + \varepsilon_3 + \cdots + \varepsilon_{2i} + \varepsilon_{2i+1})} \leq (1 + \varepsilon_1 + \varepsilon_3 + \cdots + \varepsilon_{2n-1} + \varepsilon_{2n+1})\sum_{i=0}^{n}{x_iy_i}
Zadanie 5.
a) Wykaż, że [a_n,b_n] \supset [a_{n+1},b_{n+1}] gdzie n \geq 0 .
Zgodnie z zasadami metody bisekcji: I_{n+1}=[a_{n+1},b_{n+1}] = \begin{cases} {[m_{n+1},b_n], \ f(m_{n+1})f(a_n)>0} \cr {[a_n,m_{n+1}], \ f(a_n)f(m_{n+1})<0} \end{cases}
gdzie m_n = \frac{1}{2}(a_n+b_n) stąd oczywiście: [a_{n+1},b_{n+1}]\subseteq [a_n,b_n]
b) policzymy „długość” przedziału |[a_n,b_n]| , wprost z definicji metody bisekcji. Wiemy że długość przedziału jest równa różnicy jego końców.. (pominę pisanie warunków, są identyczne jak w podpunkcie a) ) |[a_{n+1},b_{n+1}]| = \begin{cases} {|[m_{n+1},b_n]| = b_n - \frac{a_n +b_n}{2} = \frac{b_n - a_n}{2} = \frac{1}{2}|[a_n,b_n]|} \cr {|[a_n,m_{n+1}]| = \frac{a_n +b_n}{2}- a_n = \frac{b_n - a_n}{2} = \frac{1}{2}|[a_n,b_n]|} \end{cases}
zatem: |[a_n,b_n]| = 2^{-1}|[a_{n-1},b_{n-1}]| = 2^{-2}|[a_{n-2},b_{n-2}]| =…= 2^{-n}|[a_0,b_0]| = 2^{-n}(b_0-a_0)
czyli.. \frac{|[a_n,b_n]|}{|[a_0,b_0]|} = 2^{-n}
c) Wykaż, że |e_n| \leq 2^{-n-1}(b_0-a_0) dla n \geq 0
Obliczenia przerwaliśmy po znalezieniu przedziału [a_n,b_n], pierwiastek \alpha na pewno się w nim znajduje.
Pierwiastek przebliżamy wzorem: \alpha = \lim_{n\to\infty} m_n czyli do połowy znalezionego przedziału, więc błąd przybliżenia jest mniejszy równy połowie długości przedziału..
Zatem |e_n|=|\alpha - m_n| \leq |[a_{n+1},b_{n+1}]| = 2^{-(n+1)}|[a_0,b_0]| = 2^{-n-1}(b_0-a_0)
Zadanie 6.
6. Ile kroków według metody bisekcji należy wykonać, żeby wyznaczyć zero \alpha z błędem bezwzględnym mniejszym niż zadana liczba \epsilon > 0 .
Czyli chcemy, aby |e_n| < \epsilon . Z zadania poprzedniego wiemy, że |e_n| \leq 2^{-n-1}(b_0-a_0) czyli:
2^{-n-1} < \frac{\epsilon}{b_0 - a_0}
2^{n+1} > \frac{b_0 - a_0}{\epsilon}
n > log_2 \frac{b_0 - a_0}{\epsilon} - 1
interesuje nas najmniejsza pewna liczba całkowita spełniająca powyższą nierównosć, więc:
k(\epsilon) = \lceil log_2 \frac{b_0 - a_0}{\epsilon} \rceil -1
Zadanie 7.
| n | m | |e_n| | \overline{|e_n|} |
|---|---|---|---|
| 0 | 6.0000000000e-02 | 4.6926359948e-03 | 1.0000000000e-02 |
| 1 | 6.5000000000e-02 | 3.0736400520e-04 | 2.5000000000e-03 |
| 2 | 6.2500000000e-02 | 2.1926359948e-03 | 6.2500000000e-04 |
| 3 | 6.3750000000e-02 | 9.4263599480e-04 | 1.5625000000e-04 |
| 4 | 6.4375000000e-02 | 3.1763599480e-04 | 3.9062500000e-05 |
| 5 | 6.4687500000e-02 | 5.1359947960e-06 | 9.7656250000e-06 |
| 6 | 6.4843750000e-02 | 1.5111400520e-04 | 2.4414062500e-06 |
| 7 | 6.4765625000e-02 | 7.2989005204e-05 | 6.1035156250e-07 |
| 8 | 6.4726562500e-02 | 3.3926505204e-05 | 1.5258789062e-07 |
| 9 | 6.4707031250e-02 | 1.4395255204e-05 | 3.8146972656e-08 |
| 10 | 6.4697265625e-02 | 4.6296302040e-06 | 9.5367431641e-09 |
| 11 | 6.4692382813e-02 | 2.5318229599e-07 | 2.3841857910e-09 |
| 12 | 6.4694824219e-02 | 2.1882239540e-06 | 5.9604644775e-10 |
| 13 | 6.4693603516e-02 | 9.6752082901e-07 | 1.4901161194e-10 |
| 14 | 6.4692993164e-02 | 3.5716926651e-07 | 3.7252902985e-11 |
| 15 | 6.4692687988e-02 | 5.1993485267e-08 | 9.3132257461e-12 |
Wygenerowane przez:
import math alpha = 0.0646926359947960 def f(x): return x * math.exp(-x) - 0.06064 def bisect(f,a,b,n,nmax): if f(b) < 0 and n == 0: raise if n > nmax: return m = (b+a)/2 e = math.fabs(alpha - m) eapprox = 2**(-n-1) * (b-a) print '| %d | %.10e | %.10e | %.10e |' % (n,m,e,eapprox) if f(m) == 0: print "f(%) = 0", m return elif f(m) < 0: bisect(f,m,b,n+1,nmax) else: bisect(f,a,m,n+1,nmax) def main(): bisect(f,0.05,0.07,0,15) if __name__ == "__main__": main()
A czemu oszacowanie liczysz od b-a, a nie od b_0-a_0?
No fakt, pomyliło mi się. Widać tu zalety upubliczniania kodu (wystarczy zmienić program w dwóch miejscach :)–drx
Zadanie 8.
(by kz)
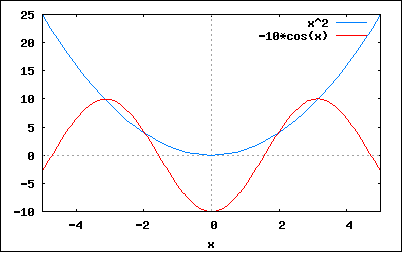
oszacowania z wykresu i reszta metodą bisekcji
funkcja jest symetryczna więc wystarczy policzyć zera po jednej stronie OY
+/- 1.96887293782
+/- 3.16195002471
from math import * def f(x): return x**2 + 10*cos(x) eps = pow(10,-12) def seek(a,b): if f(a)*f(b) > 0.: return None c = (a+b)/2. if f(c) == 0. or abs(b-a) < eps: return c elif f(a)*f(c) < 0.: return seek(a,c) else: return seek(c,b) print seek(-3.5,-3) print seek(-2.5,-1.5) print seek(1.5,2.5) print seek(3.0,3.5)