Treści
Rozwiązania
1.
G - nasz graf G' - nasza odpowiedź, początkowo tylko wierzchołki z G i żadnych krawędzi Wykonujemy kroki:
- Dla każdego wierzchołka w G znajdź najkrótszą incydentną krawędź i dodaj ją do G'
- Utwórz nowy graf G', w którym wierzchołkami są spójne składowe w starym G'
Iterujemy do póki nie zostanie jednen wierzchołek. Wszystkie dodane krawędzie do G' utworzą odpowiedź.
2.
- Kruskala - działa dobrze
- Prima - działa dobrze
- Dijkstra - Jeżeli gdzieś w grafie występuje cykl o negatywnej wadze, to wszystkie drogi nie mają najkrótszej ścieżki. Algorytm może tego nie wykryć, bo nigdy nie wraca do wierzchołków już rozważonych, a cykl możemy znaleść dopiero pod koniec wykonania, dlatego zwróci jakieś wartości dla wierzchołków, a nie powinien.
3.
Przy założeniu, że \alpha jest różna, dla każdego miejsca.
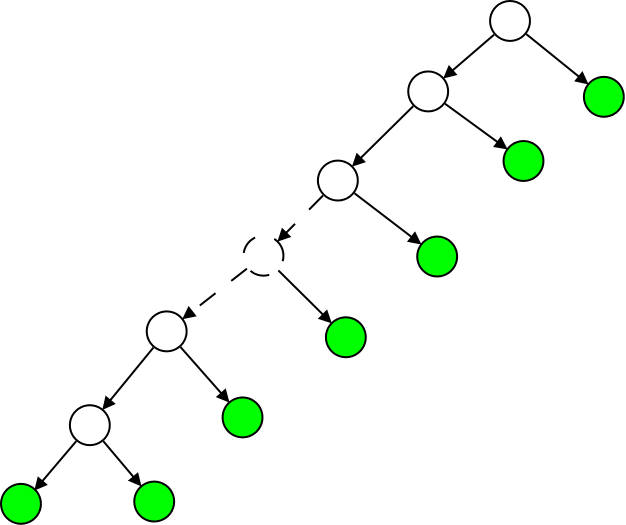
Zielone to liście.
Jeżeli skonstruujemy drzewo w taki sposób, jak na rysunku, to widzimy, zę w każdym punkcie niezmiennik jest spiełniony.
W każdym wierzchołku, który ma synów, dokonujemy podziału pozostałych elementów w stosunku (k-1):1.
Ścieżka jest liniowej długości, bo ma długość około 0.5n = O(n), czyli jest długa.
4.
Zmniejszamy wartość liścia znajdującego się na najniższym poziomie w największym drzewie w kopcu.
Jeśli wszyscy przodkowie tego liścia mają po jednym synu(czyli są zaznaczone jak mówi CLRS),
wtedy kaskadowo odcinamy każdego przodka liścia, tworząc nowe drzewo w kopcu.
Czyli liczba drzew zwiększy się o wysokość największego drzewa w kopcu.
Ta liczba wynosi k = O(\log n), bo wiemy, że drzewo o stopniu k ma wykladniczą ilość elementów, może być to jedyne drzewo, więc n=2^k.
5.
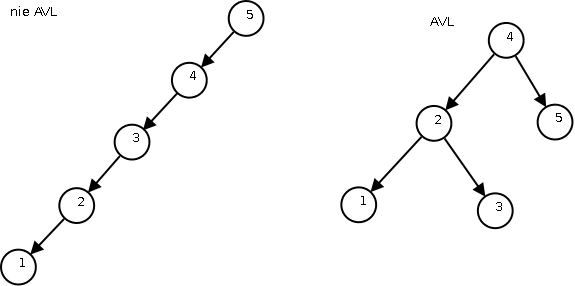
- drzewo poszukiwań binarnych - może być listą - O(n)
- drzewo AVL - niezmienniki gwarantuja zrównoważenie - O(\log n)
- kopiec - w ogóle nie ma posortowania - O(n)
- kopiec dwumianowy - j.w. - O(n)
- drzewa czerwono-czarne - jak AVL - O(\log n)
6.
\displaystyle T(1)=1
\displaystyle T(2)=3
\displaystyle T(n)=T(n-2)+2n-1=T(n-2)+n+(n-1) dla n >2
\displaystyle T(n)=n+(n-1)+T(n-2)=
\displaystyle n+(n-1)+(n-2)+(n-3)+T(n-4)=
\displaystyle n+(n-1)+(n-2)+(n-3)+\cdots+4+3+2+1=
\displaystyle \frac {n(n+1)} 2
7.
quicksort - jeżeli znajdowanie pivota jest źle zrobione, tzn. odcina stałą liczbę elementów przy każdym partition,
np. stosunek 1:(n-1), to wtedy złożoność to n*O(n) = O(n^2)
mergesort - worst case O(n\log n)
insertsort - posortowany lub odwrotnie posortowany ciag bedzie mieć O(n^2)
8.
Składniki
T(\lceil n/5\rceil) - podczas algorytmu dzielimi elementy na piątki, w każdej piątce znajdujemy mediane i rekurencyjnie wybieramy mediane z tych \lceil n/5 \rceil median, aż zostanie jedna wartość
T(\lceil 7n/10\rceil) - jak znalezliśmy już mediane median z kroku wyżej, to wiemy z przechodniości mniejszości, że ten element jest wiekszy od conajmniej 3n/10 elementów (w każdej piątce mediana była więksa od 2 elementów, my bierzemy mediane median, czyli w połowie piątek nasz element był wiekszy od 3 elementów).
O(n) - koszt przejscia przez elementy i znalezienia median piątek
Dlaczego jest θ(n)
T(n) \leq T(1n/5)+T(7n/10)+O(n)=
c(4n/20 + 14n/20)+O(n)=
cn - (2n/20 - O(n)) \leq cn
Dobieramy c na tyle duże, żeby pasowało do wartości kosztu obu wywołań.
9.
Pivot jest w A[p], funkcja zwaraca granicę podziału
Part(A[1..n], p, r)
x <- A[p]
i <- p-1
j <- r+1
while(i<j) do
repeat(j--) until A[j] <= x
repeat(i++) until A[i] >= x
if(i<j) swap(A[i], A[i])
else return j
11.
Problem: Wybrać najmniejszy taki podzbiór z rodziny zbiorów, aby wszystkie pojedyncze elementy z całej rodziny znalazły sie w tym podzbiorze.
Algorytm aproksymacyjny: W każdym kroku odrzucamy zbiór, który nie pokrywa jak nawiekszej części elementów.
Tzn.:
U - uniwersum do pokrycia
R - wejsciowa rodzina zbiorow
W - wynikowa rodzina zbiorow na poczatu pusta
while U jest niepusty
wybierz takie Z z R ze Z ∩ U jest maksymalne
dodaj Z do rodziny wynikowej W
U \= Z
usun Z z R
12.
Tyle ile jest binarnych carry podczas dodawania 35 i 53.
0100011
0110101
——-
1011000
Wychodzi mi 4.
13.
Niech H będzie rodziną funkcji hashujących z U w \{0,…,m-1\}.
Rodzinę H nazywamy uniwersalną,
jeśli \forall_{x,y\in U ;x\neq y} |{h \in H : h(x)=h(y)}|= \frac {|H|} m
14.
Wiemy, że dla jednego setu priorytetów i kluczy mamy jednego możliwego drzewca.
Zakładamy raz, że jeden z równych priorytetów jest wyższy - mamy 1. drzewca,
potem zakładamy, że jest niższy - mamy 2. drzewca.
Odp. 2 drzewce.
15.
Żeby zachować niezmienniki potrzebne do amortyzowanej złożoności, nie pozwalamy w operacji odcięcia,
usunięcia więcej niż jednego poddrzewa z jednego wierzchołka.
Dlatego zaznaczamy ojca, który utracił jednego syna
i przy próbie usunięcia mu kolejnego syna usuwamy całe poddrzewo i dodajemy je do ogólnej listy.
Po tym markujemy jego dziadka (jeżeli jest zmarkowany, to znowu usuwamy poddrzewo i rekurencyjnie w gore).
16.
Mamy n-elementowy kopiec w wersji lazy. Robimy deletemin.
W najgorszym przypadku minimum będzie w korzeniu największego drzewa w kopcu.
Wysokość tego drzewa to k = {\lfloor log_2{n}\rfloor} + 1.
Wielkość tego drzewa to oczywiście 2^{\lfloor log_2{n}\rfloor}.
Wiadomo też z definicji drzewa dwumianowego, że drzewo wysokości k posiada k-1 synów,
z których każdy jest korzeniem drzewa wysokości kolejno k-1,k-2,…, 1.
Zatem usuwając minimum z drzewa o wysokości k dodajemy do kopca k-1 = \lfloor log_2{n}\rfloor nowych drzew.
17.
Liczymy iloczyny macierzy dla każdego a_i•b_i.
Takich iloczynów jest oczywiscie \frac{n}{\log(n)},
a każdy w wyniku daje jedną macierz kwadratową. Jeśli zsumujemy
te macierze to
otrzymamy iloczyn, o który nam chodzi.
18.
Graf przechodzimy przy pomocy rekurencyjnej procedury DFS. Przebyte krawędzie usuwamy, a wierzchołki po zakończeniu przetwarzania umieszczamy na początku kolejki. Jeśli graf posiada cykl Eulera, to po zakończeniu algorytmu w kolejce znajdą się kolejne wierzchołki tego cyklu.
19.
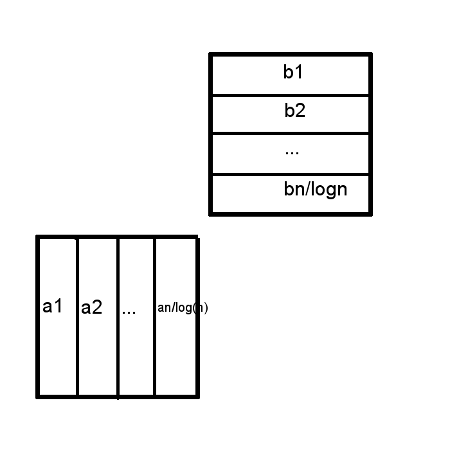
I assume, że
n kluczy rozrzucamy do m różnych tablic jedną funkcją hashującą. Potem w każdej z m tablicy hashujemy elementy zamiast tworzyć listę elementów.
Czyli potrzeba m+1 funkcji hashujących.
jeśli to jest dobrze to po co dali mi informację o ilości kluczy?
21.
| a | b | r | a | k | a | d | a | b | r | a |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 2 | 3 | 4 |
22.
Automat jest niedeterministyczny, zielone stany to stany akceptujące.
23.
Przy zastosowaniu tylko kompresji ścieżki, koszt UNIONa pozostaje O(1). Analiza kosztu FINDa jest bardziej skomplikowana (przedstawiona w poniższym pliku).
źródło:http://www.mpi-inf.mpg.de/~mehlhorn/ftp/Toolbox/MinimumSpanningTrees.pdf, kopia lokalna: minimumspanningtrees.pdf
(Theorem 11.5.) mówi, że całkowity koszt to: O((m+n) \log n).
Ogólnie ten pdf to fragment książki „Algorithms and Data Structures: The Basic Toolbox” - Kurt Mehlhorn,Peter Sanders
24.
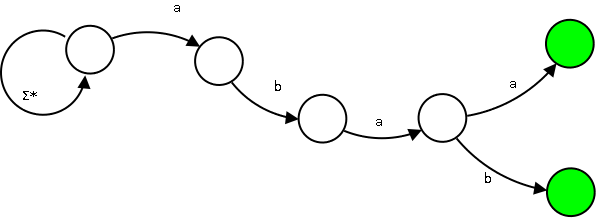
SHIFT-OR algorytm
Niechaj T to będzie nasz tekst. m - długość wzorca W.
1. Każdej literze \alpha z alfabetu przyporządkowujemy wektor S_{\alpha} długości m, gdzie S_{\alpha}[i] = 0 iff W[i] = \alpha, w przeciwnym razie 1.
2.
Tworzymy wektor bitowy V_0 długości m, składający się z samych 1. Potem go SHIFTujemy i ORujemy z wektorem pierwszej literki.
Czyli V_{0} = ( SHIFTV_0) OR S_{T[0]}
3.
Następnie robimy tak: V_{i+1} = ( SHIFTV_i) OR S_{T[i+1]} - Czyli najpierw SHIFTujemy a potem ORujemy z wektorem kolejnej litery w tekście.
Dopasowanie wzorca dostaniemy gdy ostatni bit wektora V_i się równa zero, czyli V_i[m-1] = 0
Ten cały SHIFT to jest SHIFT-RIGHT!!
25.
Mamy grafy A i B w postaci macierzy adjacencji.
Możemy korzystać z algebry, w której:
'+' to działanie \min
'\cdot' to dodawanie
Wtedy jedno mnożenie macierzy, to jeden krok relaksacji najkrótszych ścieżek,
musimy wykonać n takich relaksacji. Złożoność O(n^4).
Można poprawić złożoność.
Nie da sie zastosować algorytmu Strassena, bo nie mamy działania odwrotnego do \min.
Można za to skorzystać z szybkiego potęgowania, co zmniejsza nam koszt do O(n^3\log n).
26.
Mamy wielomian A(x) stopnia n, reprezentowany przez współczynniki a_0, a_1, \cdots, a_n.
Tworzymy 2 nowe wielomiany:
A^{[0]}(x)=a_0 + a_2 x + a_4 x^2 + … a_{n-2} x^{n/2 -1} + a_n x^{n/2}
A^{[1]}(x)=a_1 + a_3 x + a_5 x^2 + … a_{n-1} x^{n/2 -1}
A(x) = A^{[0]}(x^2)+xA^{[1]}(x^2)
To tyle?
27.
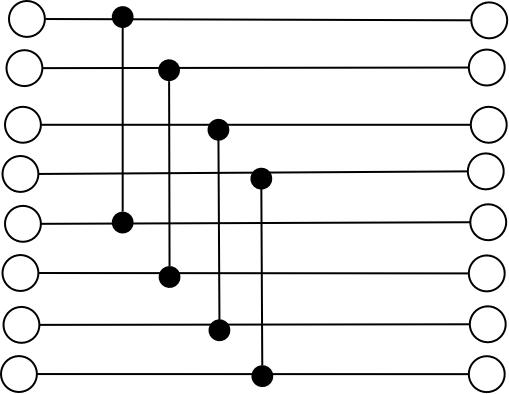
Powiedzmy, ze mamy dodac 2 liczby n-bitowe i zalozmy ze mamy policzony wektor przeniesien:
c_{n+1} c_{n}…c_{3} c_{2} c_{1} c_{0}
b_{n}…b_{3} b_{2} b_{1} b_{0}
+a_{n}…a_{3} a_{2} a_{1} a_{0}
wtedy wynik dodawania wyraza sie wzorem d_i = a_i xor b_i xor c_i
Teraz zobaczmy ze gdy a_i = b_i = 0 to c_{i+1} = 0 oraz gdy
a_i = b_i = 1 to c_{i+1} = 1 niezaleznie od tego jaki jest remainder c_i.
Ale takze gdy a_i = 1 b_i = 0 lub na odwrot to wtedy c_{i+1} = c_i.
Wiec zdefiniujemy sobie dzialanie * na zbiorze X = {0, 1, p}
dzialajace dokladnie jak powyzej czyli dla kazdego x ze zbioru X mamy:
0 * x = 0 - ustaw na 0
1 * x = 1 - ustaw na 1
p * x = x - przepisz to co masz z prawej strony
to dokladnie odpowiada trzem przypadkom jakie mielismy powyzej
dzialanie jest lacznie ale nie przemienne.
Teraz z wektorem przeniesien mozemy zwiazac wyrazenie:
czyli gdy mamy a_i = 1 b_i = 0 lub na odwrot to x_i = p lub
a_i = b_i = 1 to x_{i+1} = 1 lub a_i = b_i = 0 to x_{i+1} = 0
Zatem z wektorem przeniesien zwiazujemy wyrazenie x_{n+1} * x_n * … * x_0 gdzie x_i∈X sa wyliczone jak powyzej.
Jesli moglibysmy policzyc wszystkie y_i = c_i = x_i * … * x_0 w czasie logn z uzyciem
wielu procesorow to mielibysmy wektor przeniesien wiec caly problem rozwiazalibysmy
w czasie O(1 + logn).
Jak to policzyc jest zaprezentowane na rysunku:
