Compiler Construction - Lista 3.
Zadanie 2.
a) (\sum | balicki )^*
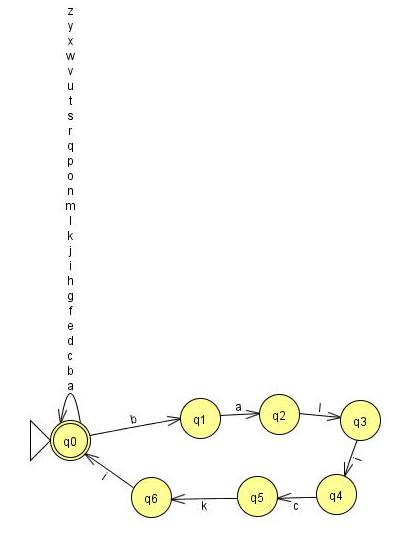

e) Because balicki^* can be created by \sum^*, because every word from language can be created from it.
Zadanie 3.
Lemat o pompowaniu dla jezyków regularnych Dla kazdego jezyka regularnego L istnieje liczba n nalezaca do N (zwana “stała z lematu o pompowaniu”, odpowiadajaca liczbie stanów pewnego DFA) taka, ze dla kazdego słowa w nalezacego do L takiego, ze |w| >= n istnieje taki podział w = w_1w_2w_3 takie, ze |w_1w_2| \leq n, |w2| >= 1 i dla kazdego k nalezacego do N słowo w_1(w_2^k)w_3 nalezy do L.
Niech n - stała z lematu o pompowaniu dla języków regularnych. Rozważmy w = (^{2n})^{2n}. Ponieważ w należy do L oraz |w| \geq n, więc istnieje podział w = w_1w_2w_3 spełniający założenia lematu. Z postaci w widzimy, że w_1 = (^m, w_2 = (^p, w3 = (^q)^{2n}. Z lematu wiemy, że \forall_k v = w_1(w_2^k)w_3 należy do L. Ale v = (^{m+p*k+q} )^{2n} i dla k > 1, m+p \cdot k+q > 2n, co oznacza, że v zawiera więcej '(' niż ')', więc nie należy do L. Otrzymana sprzeczność dowodzi, że L nie jest regularny, a więc nie istnieje wyrażenie regularne opisujące ten język.