Rachunek prawdopodobieństwa i statystyka - Lista 4.

Ale fajna lista :D

f(x,y) = Cxy + x + y, 0 \leq x \leq 2, 0 \leq y \leq 1.

f musi się sumować do 1, sprawdźmy to więc.

\displaystyle \int_x \int_y f(x,y) dy dx = \int_0^2 \int_0^1 (Cxy + x + y) \; dy \; dx = \int_0^2 (\frac {Cx} 2 + x + \frac 1 2) dx = C + 2 + 1 = C + 3

Więc C = -2.

Problem w tym, że nie wiem czy wartość funkcji gęstości może kiedykolwiek przyjmować wartość ujemną. Na pierwszy rzut oka nie, ale zapytam WKa i do tego czasu spauzuję.

Update: Nie może. A f(2,1) = -2 \cdot 2 \cdot 1 + 2 + 1 = -1. Więc nie da się wyznaczyć takiego C.

f(x,y) = Cxy + x, 0 \leq x \leq 2, 0 \leq y \leq 1.

\displaystyle 1 = \int_x \int_y f(x,y) dy dx = \int_0^2 \int_0^1 (Cxy + x) \; dy \; dx = \int_0^2 (\frac {Cx} 2 + x) dx = C + 2

Więc C = -1.

f(x,y) = -xy + x = x(1-y). x \geq 0 oraz 1-y \geq 0 więc funkcja ma poprawny zbiór wartości.

Policzmy f. brzegowe.

\displaystyle f_X(x) = \int_y f(x,y) = \int_0^1 (-xy+x) \; dy = \frac {-x} 2 + x = \frac x 2

\displaystyle f_Y(y) = \int_x f(x,y) = \int_0^2 (-xy+x) \; dx = -2y + 2

\displaystyle f_X(x) \cdot f_Y(y) = \frac x 2 \cdot (-2y + 2) = -xy + x = f(x,y). Czyli X i Y są niezależne.

Teraz zabieżmy się za ostatni podpunkt.

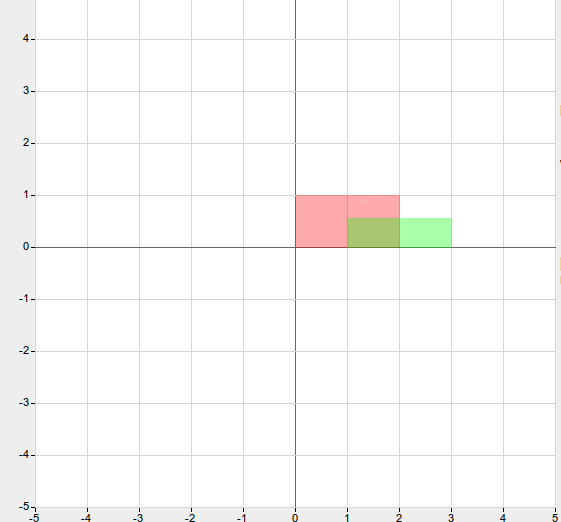
Na czerwono jest region w którym funkcja jest zdefiniowana (czyli tam gdzie być może przyjmuje niezerowe wartości, wszędzie indziej jest zero). Na zielono jest obszar który nas interesuje.

A więc \displaystyle P(1 \leq X \leq 3, 0 \leq Y \leq 0.5) = P(0 \leq X \leq 2, 0 \leq Y \leq 0.5) - P(0 \leq X \leq 1, 0 \leq Y \leq 0.5) = \int_0^2 \int_0^{0.5} (-xy+x) \; dy \; dx - \int_0^1 \int_0^{0.5} (-xy+x) \; dy \; dx = \int_0^2 \frac {3x} 8 dx - \int_0^1 \frac {3x} 8 dx = \frac 3 4 - \frac 3 {16} = \frac 9 {16}

f(x,y) = C(x+y)e^{-(x+y)}, x>0, y>0

\displaystyle 1 = \int_x \int_y f(x,y) \; dy \; dx = \int_0^{\infty} \int_0^{\infty} C(x+y)e^{-(x+y)} \; dy \; dx = \int_0^{\infty} Cx \int_0^{\infty} e^{-(x+y)} \; dy \; dx + \int_0^{\infty} \int_0^{\infty} Cy \cdot e^{-(x+y)} \; dy \; dx = \int_0^{\infty} Cx e^{-x} \int_0^{\infty} e^{-y} \; dy \; dx + \int_0^{\infty} C e^{-x} \int_0^{\infty} y \cdot e^{-y} \; dy \; dx =

\displaystyle = \int_0^{\infty} Cx e^{-x} \; dx + \int_0^{\infty} C e^{-x} \; dx = C + C = 2C

Czyli C = \frac 1 2.

Policzmy f. brzegowe. Zauważmy, że już to zrobiliśmy wyżej.

\displaystyle f_X(x) = \int_0^{\infty} \frac 1 2 (x+y)e^{-(x+y)} dy = \frac 1 2 x e^{-x} + \frac 1 2 e^{-x}

\displaystyle f_Y(y) = \int_0^{\infty} \frac 1 2 (x+y)e^{-(x+y)} dx = \frac 1 2 x e^{-y} + \frac 1 2 e^{-y}. Przypadek bardzo analogiczny. Ciekawe czy to ma jakiś związek z „symetrycznością” f; strzelam, że tak.

\displaystyle f_X(x) \cdot f_Y(y) = \frac 1 4 (x+1) (y+1) e^{-x-y} \neq f(x,y). Czyli X i Y są zależne.

Nie wiem co to m_{10}, etc., ale dowiem się, być może macierz kowariancji.

m_{NL} to moment. Dodatkowo: m_{10} = E(X), m_{01} = E(Y), m_{11} = E(X \cdot Y)

Ogólny wzór na moment to \displaystyle m_{NL} = \int_{\infty}^{\infty} \int_{\infty}^{\infty} x^{N} \cdot y^{L} \cdot f(x, y) \; dx \; dy

Tutaj chyba powinno wyjść m_{10} = m_{01}

Teraz policzmy współczynnik korelacji.

\displaystyle \rho_{X,Y} = \frac {cov(X,Y)} {\sigma_X \sigma_Y} = \frac {E(X\cdot Y) - E(X)E(Y)} {\sqrt{E(X^2)-E(X)^2} \sqrt{E(Y^2)-E(Y)^2}} ZOMG dużo liczenia.

W tym zadaniu przyda nam się całka:

\displaystyle \int_{-\infty}^{\infty} \exp \left\{ -\frac12 \left( \frac{x + a}{b} \right)^2 \right\} = b\sqrt{2\pi}

Powyższą całkę piszę z pamięci – do weryfikacji. WKA ją podał jako uogólnienie takiej całki dla a = 0, b = 1.

\displaystyle f(x,y) = C e^{- \frac 1 2 (x^2 + 2xy + 5y^2)}

\displaystyle 1 = \int_x \int_y f(x,y) \; dy \; dx = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} cdn

Tutaj można zrobić troche na opak. Trzeba się zastanowić nad zadaniem – z treści wynika, że X i Y są niezależne, więc najpierw budujemy f_X(x) i f_Y(y), a potem wyznaczamy po prostu f(x,y) = f_X(x)f_Y(y).

		X	0	1	2	3
		f_X(X)	\frac 1 4	\frac 1 4	\frac 1 4	\frac 1 4
Y	f_Y(Y)	f(x,y)
0	\frac 3 6		\frac 3 {24}	\frac 3 {24}	\frac 3 {24}	\frac 3 {24}
3	\frac 1 6		\frac 1 {24}	\frac 1 {24}	\frac 1 {24}	\frac 1 {24}
4	\frac 1 6		\frac 1 {24}	\frac 1 {24}	\frac 1 {24}	\frac 1 {24}
5	\frac 1 6		\frac 1 {24}	\frac 1 {24}	\frac 1 {24}	\frac 1 {24}

cdn :P