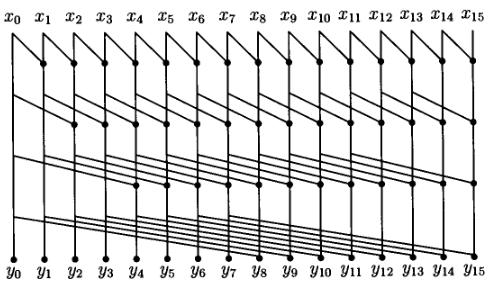
27.
Powiedzmy, ze mamy dodac 2 liczby n-bitowe i zalozmy ze mamy policzony wektor przeniesien:
c_{n+1} c_{n}…c_{3} c_{2} c_{1} c_{0}
b_{n}…b_{3} b_{2} b_{1} b_{0}
+a_{n}…a_{3} a_{2} a_{1} a_{0}
wtedy wynik dodawania wyraza sie wzorem d_i = a_i xor b_i xor c_i
Teraz zobaczmy ze gdy a_i = b_i = 0 to c_{i+1} = 0 oraz gdy
a_i = b_i = 1 to c_{i+1} = 1 niezaleznie od tego jaki jest remainder c_i.
Ale takze gdy a_i = 1 b_i = 0 lub na odwrot to wtedy c_{i+1} = c_i.
Wiec zdefiniujemy sobie dzialanie * na zbiorze X = {0, 1, p}
dzialajace dokladnie jak powyzej czyli dla kazdego x ze zbioru X mamy:
0 * x = 0 - ustaw na 0
1 * x = 1 - ustaw na 1
p * x = x - przepisz to co masz z prawej strony
to dokladnie odpowiada trzem przypadkom jakie mielismy powyzej
dzialanie jest lacznie ale nie przemienne.
Teraz z wektorem przeniesien mozemy zwiazac wyrazenie:
czyli gdy mamy a_i = 1 b_i = 0 lub na odwrot to x_i = p lub
a_i = b_i = 1 to x_{i+1} = 1 lub a_i = b_i = 0 to x_{i+1} = 0
Zatem z wektorem przeniesien zwiazujemy wyrazenie x_{n+1} * x_n * … * x_0 gdzie x_i∈X sa wyliczone jak powyzej.
Jesli moglibysmy policzyc wszystkie y_i = c_i = x_i * … * x_0 w czasie logn z uzyciem
wielu procesorow to mielibysmy wektor przeniesien wiec caly problem rozwiazalibysmy
w czasie O(1 + logn).